Futures are standardized bilateral contracts of agreement to buy or sell an asset at a pre-determined price at a pre-specified time in the future. The underlying assets can be physical commodities, market indexes, or financial instruments. The Chicago Mercantile Exchange (CME), which is the world’s largest futures exchange, averages well over 15 million futures contracts traded per day.
In the futures market, it is commonly observed that the futures prices may deviate from the spot price of the underlying asset. The differential between futures and spot prices, called the basis, can be positive or negative but are expected to converge to zero or near-zero at the expiration of the futures contract.
For each underlying asset, there are multiple futures with different maturities (ranging from 1 month to over a year). And for each futures contract, there is one basis process. Therefore, when we consider all different spot assets and their associated futures, there are a high number of basis processes.
Moreover, these stochastic processes are clearly dependent.
First, different underlying assets, such as silver and gold, can be correlated. Second, the futures contracts written on the same underlying asset are clearly driven by a common source of randomness, among other factors. For anyone trading futures — on the same underlying or different assets — it is crucial to understand the dependence structure among these processes.
Multidimensional Scaled Brownian Bridge
This motivates us to develop a novel model to capture the joint dynamics of stochastic basis from different underlying assets and different futures contracts. Once this model is built, one can apply it to dynamic futures trading, as studied in this paper:
B. Angoshtari and T. Leung, Optimal Trading of a Basket of Futures Contracts [pdf; link], Annals of Finance, 2020
The Multidimensional Scaled Brownian Bridge (MSBB) is a continuous-time stochastic model described by the following multidimensional stochastic differential equation (SDE):
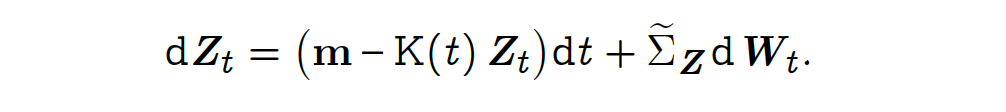
where
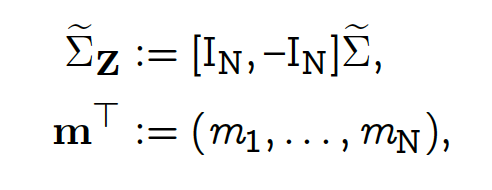
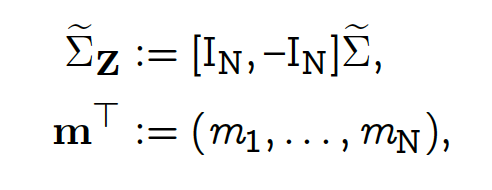
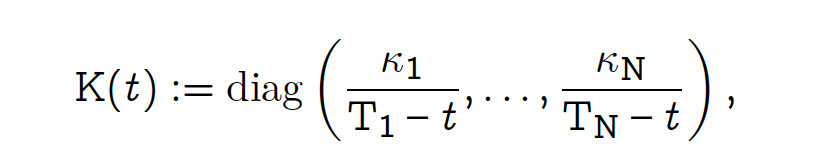
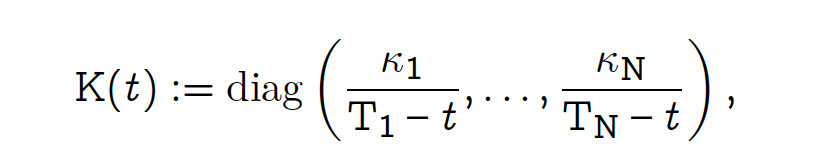
and W consists of Brownian motions.
In fact, Z is a N-dimensional process where each component is a 1-dimensional scaled Brownian bridge:
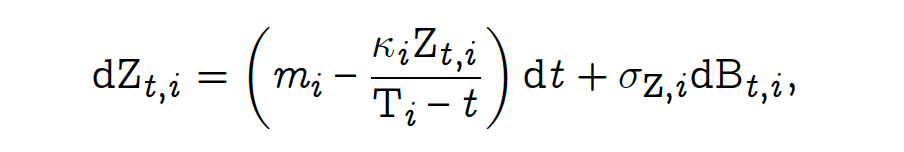
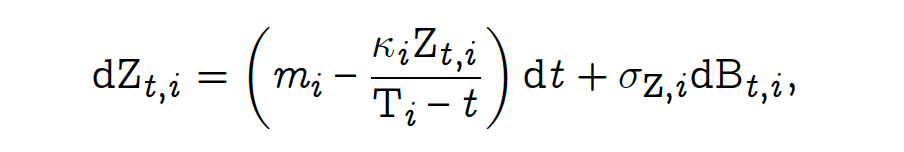
The stochastic differential equation for a 1-d scaled Brownian bridge. Note that the scaled Brownian bridges Zᵢ are correlated.
The SDE for the multidimensional scaled Brownian bridge has a unique solution
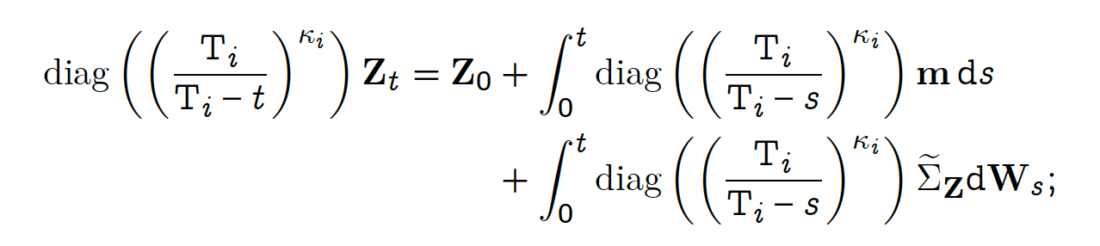
Here, we used the shorthand notation for the diagonal matrix: diag (aᵢ ) = diag(a₁ , . . . , aN).
The mean function of Z is given by
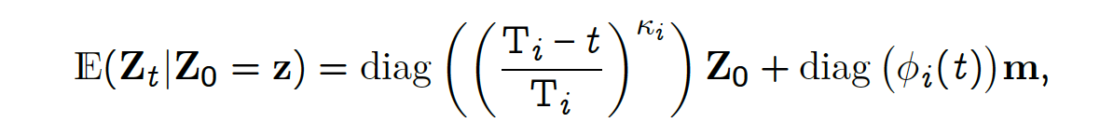
where
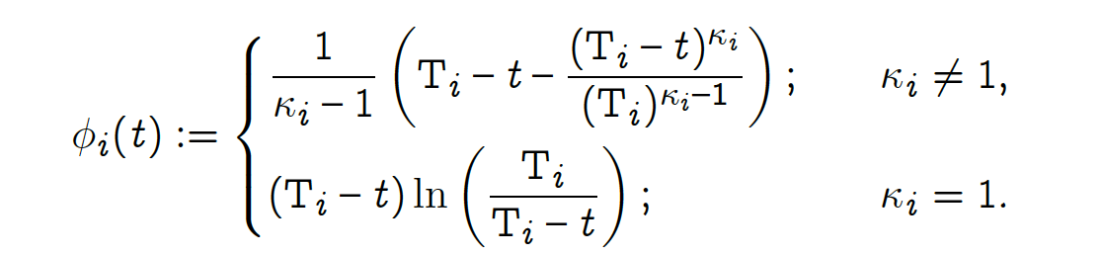
κᵢ is the scaling parameter.
And the covariance function is
Figure 1 illustrates the simulated paths of Z, S, and F for two pairs of futures and underlying assets (i.e. N = 2). Here, each Z is the log basis (i.e. log(F/S)) for the corresponding asset and futures contract. The plots for (Zt,1) and (Zt,2) also show the 95% confidence intervals of the log-bases.
Figure 1: Simulated sample paths of S and F for two pairs of futures and spot (i.e. N = 2), and the corresponding 2-dimensional basis processes Z. Source: Angoshtari and Leung (2020), available at https://arxiv.org/pdf/1910.04943.pdf
These plots showcase two characteristics of the log-bases. First, they are mean-reverting in that any deviation from their mean is corrected. Second, they partially converge to zero at the end of the trading horizon (T = 0.25) as evident by narrowing of the confidence intervals. Indeed, (Zt,1) and (Zt,2) are Brownian bridges that converge to zero at T₁ = 0.27 and T₂ = 0.254, respectively. This convergence is not realized since trading stops at T = 0.25 in this particular example.
Since, Zt|Z₀ is a multivariate normal random variable, this means that
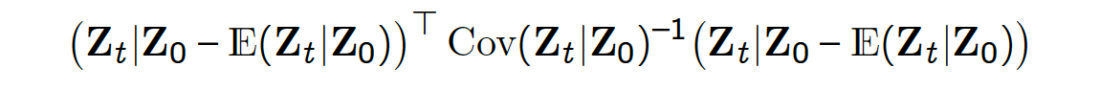
has a chi-squared distribution with N degrees of freedom. This relationship is utilized for obtaining the 95% confidence regions of Zt represented by dashed blue ellipses. These plots also illustrate partial convergence of log-basis at the end of time horizon.
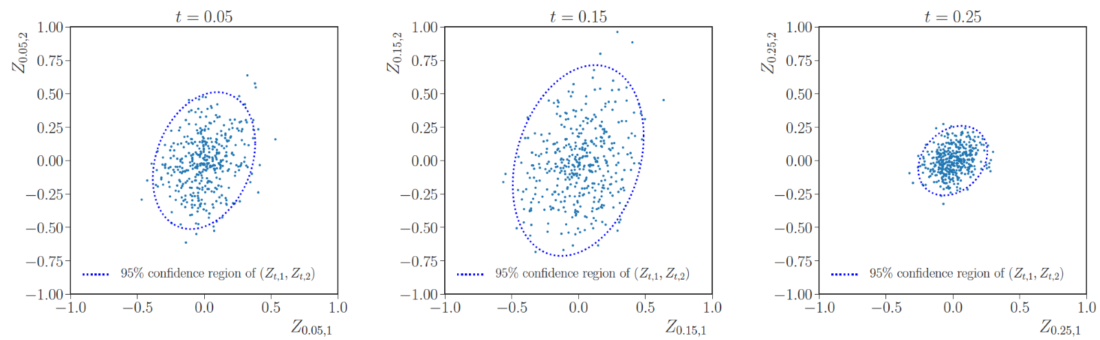
Simulated values of (Z₁, Z₂ ) based on 400 Simulated paths observed at three different times: t = 0.05 (left), t = 0.15 (middle), and t = 0.25 (right). The dotted lines represent the border of the 95% confidence region for (Z₁, Z₂), conditional on Z₀ = (0,0). Source: Angoshtari and Leung (2020), available at https://arxiv.org/pdf/1910.04943.pdf
Simulation
The SDE solution for the multidimensional scaled Brownian bridge actually lends itself to a simulation algorithm. We refer to the paper for details, but the main idea is to discretize the time horizon in M time steps, simulate independent Gaussian random variables, and put them in the right places as follows:
Source: Angoshtari and Leung (2020), available at https://arxiv.org/pdf/1910.04943.pdf
For any notations not explained herein, please refer to the papers below.
Takeaways
For trading systems that involve multiple futures and assets, it is imperative to properly capture the dependence among price processes. MSBB described herein is designed for modeling the joint dynamics among futures and their spot assets. Through the solution to the stochastic differential question, this model is straightforward to simulate. With simulated sample paths, one can test the performance of trading strategies.
For research discussions, reach out to Prof. Leung here.
References
B. Angoshtari and T. Leung, Optimal Trading of a Basket of Futures Contracts [pdf; link], Annals of Finance, 2020
B. Angoshtari and T. Leung, Optimal Dynamic Basis Trading [link; read online], Annals of Finance, Vol.15, Issue 3, pp. 307–335, 2019
Disclosure: Interactive Brokers
Information posted on IBKR Campus that is provided by third-parties and not by Interactive Brokers does NOT constitute a recommendation by Interactive Brokers that you should contract for the services of that third party. Third-party participants who contribute to IBKR Campus are independent of Interactive Brokers and Interactive Brokers does not make any representations or warranties concerning the services offered, their past or future performance, or the accuracy of the information provided by the third party. Past performance is no guarantee of future results.
This material is from Computational Finance & Risk Management, University of Washington and is being posted with permission from Computational Finance & Risk Management, University of Washington. The views expressed in this material are solely those of the author and/or Computational Finance & Risk Management, University of Washington and IBKR is not endorsing or recommending any investment or trading discussed in the material. This material is not and should not be construed as an offer to sell or the solicitation of an offer to buy any security. To the extent that this material discusses general market activity, industry or sector trends or other broad based economic or political conditions, it should not be construed as research or investment advice. To the extent that it includes references to specific securities, commodities, currencies, or other instruments, those references do not constitute a recommendation to buy, sell or hold such security. This material does not and is not intended to take into account the particular financial conditions, investment objectives or requirements of individual customers. Before acting on this material, you should consider whether it is suitable for your particular circumstances and, as necessary, seek professional advice.
In accordance with EU regulation: The statements in this document shall not be considered as an objective or independent explanation of the matters. Please note that this document (a) has not been prepared in accordance with legal requirements designed to promote the independence of investment research, and (b) is not subject to any prohibition on dealing ahead of the dissemination or publication of investment research.
Any trading symbols displayed are for illustrative purposes only and are not intended to portray recommendations.
Disclosure: Futures Trading
Futures are not suitable for all investors. The amount you may lose may be greater than your initial investment. Before trading futures, please read the CFTC Risk Disclosure. A copy and additional information are available at ibkr.com.
