Dynamic Futures Portfolio in a Regime-Switching Market

Regime-Switching Market 

Asset prices are often seen as being dependent on market conditions. Market regimes may change suddenly and persist for a period of time. The unpredictability of the timing of regime changes also means that associated risks are almost impossible to hedge. 

In order to capture these crucial properties of market dynamics, one major approach is to represent stochastic market regimes by a finite-state Markov chain. In most cases, the Markov chain is an exogenous random process and is not directly tradable. The effects of the Markov chain are reflected in the asset price dynamics. In particular, the asset’s expected return and volatility may vary across regimes. 

Regime-switching time series models have been used for decades. In addition to representing asset price dynamics through changing market conditions, regime-switching models have been applied to many problems in economics and finance, including derivatives pricing and portfolio selection. 

Futures Trading Problem 

In our new paper, we present a stochastic control approach to generate dynamic futures trading strategies. We consider a general regime-switching framework in which the stochastic market regime is represented by a continuous-time finite-state Markov chain. The underlying asset’s spot price is modeled by a Markov modulated diffusion process. 

Under the regime-switching market framework, we first derive the no-arbitrage price dynamics for the futures contracts and provide a numerical method to compute the prices. 

Next, we determine the optimal futures trading strategy by solving a stochastic control problem. Our portfolio optimization approach allows for trading different numbers of futures. By analyzing and solving the associated Hamilton-Jacobi-Bellman (HJB) equations, we derive the investor’s optimal futures position over time as a function of time, spot price, and market regime. 

Regime-Switching Mean-Reverting Model 

Our general framework captures many different regime-switching models. For example, we introduce the Regime-Switching Exponential Ornstein-Uhlenbeck (RS-XOU) model that is mean-reverting as well as regime-switching. The log price of the underlying asset follows the stochastic differential equation: 

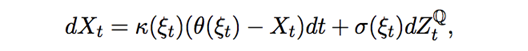
where the coefficients are functions of ξ, a continuous-time irreducible finite-state Markov chain with state-space E = {1, 2, . . . , M}. 

In a two-regime example, we simulate a scenario where the market starts in regime 2, then switches to regime 1 (at time t1) before returning to regime 2 (at time t2). Sample paths of the futures prices and optimal positions are shown below. 

Sample paths of the spot price, T1-futures price, and T2-futures price over the trading horizon under the RS-XOU model. The market starts in regime 2, then switches to regime 1 at time t1, before switching back to regime 2 at time t2. Source: T. Leung and Y. Zhou (2019) available at https://arxiv.org/abs/1910.06432. 

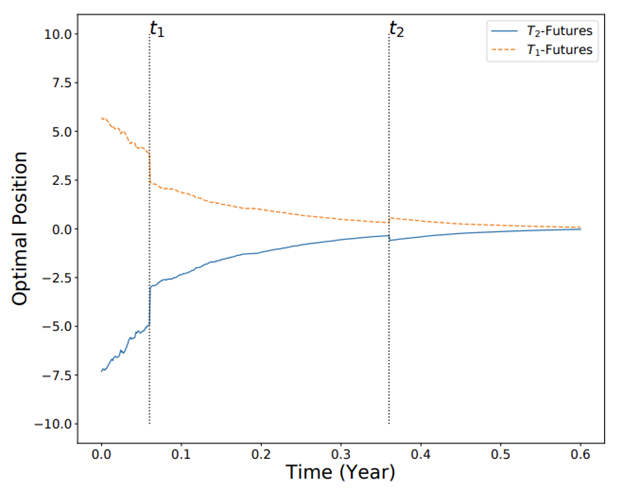
Sample paths of the optimal positions in the T1-futures and T2-futures respectively under the RS-XOU model. The futures positions tend to decrease over time and approach zero near the end of the trading horizon. Jumps in both positions occur at the regime-switching times t1 and t2. Source: T. Leung and Y. Zhou (2019) available at https://arxiv.org/abs/1910.06432. 

References 

T. Leung and Y. Zhou (2020), A Stochastic Control Approach to Futures Trading with Regime Switching [link], in the Proceedings of the American Control Conference 

T. Leung and Y. Zhou (2019), Optimal Dynamic Futures Portfolio in a Regime-Switching Market Framework [pdf], International Journal of Financial Engineering, Vol. 6, №4, p.1950034 

Google Scholar // Linkedin Page // Homepage