Investors have positive preferences for odd moments (mean, skewness) and negative preferences for even moments (variance, kurtosis). This is well known, but did you know that also statisticians like higher order moments?
At the 2022 R/Finance conference, Professor Kris Boudt explains why. He takes the case of predicting the US equity risk premium using statistical factors extracted from the 134 macro-economic variables in the FRED-MD database. Together with Guanglin Huang and Wanbo Lu, he has developed a framework to do a PCA-like analysis on coskewness and cokurtosis matrices instead of the covariance matrix. They find superior factor selection and estimation performance when the error variation in the macro-economic data is large compared to the factor variation. This is a setting researchers refer to as “weak factors”.
The method is simple. Suppose that the multivariate time series data is stored in the T × N matrix X, and that the data have been centered such that they have zero mean. The matrix X is high-dimensional (large N) and researchers want to extract a small number of factors that drive the comovement in the data. Formally, the view is that X can be decomposed as X = FΛT + E with F the factor data matrix, and the number of factors being much smaller that the number of variables. The matrix Λ is the loading matrix and E is the matrix with idiosyncratic variation. Only X is observed. Finding the Λ, F and E matrices is the econometric magic of statistical factor analysis.
Standard PCA uses the eigenvalues and eigenvectors of XT X. In the ideal case, there is a clear separation between the eigenvalues of the factors and those of the error terms in the screeplot showing the ordered eigenvalues:
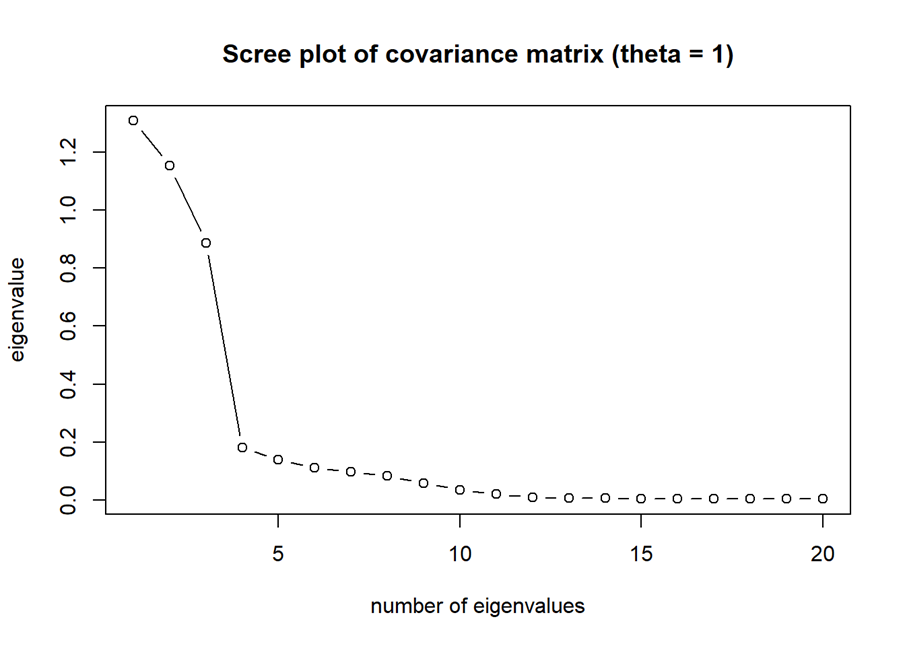
Source: Kris Boudt (R/Finance 2022 presentation)
This does not work anymore when a lot of variation in X is driven by the error variation E. Indeed, if one computes the screeplot in the case of weak factors, the typical scree plot becomes
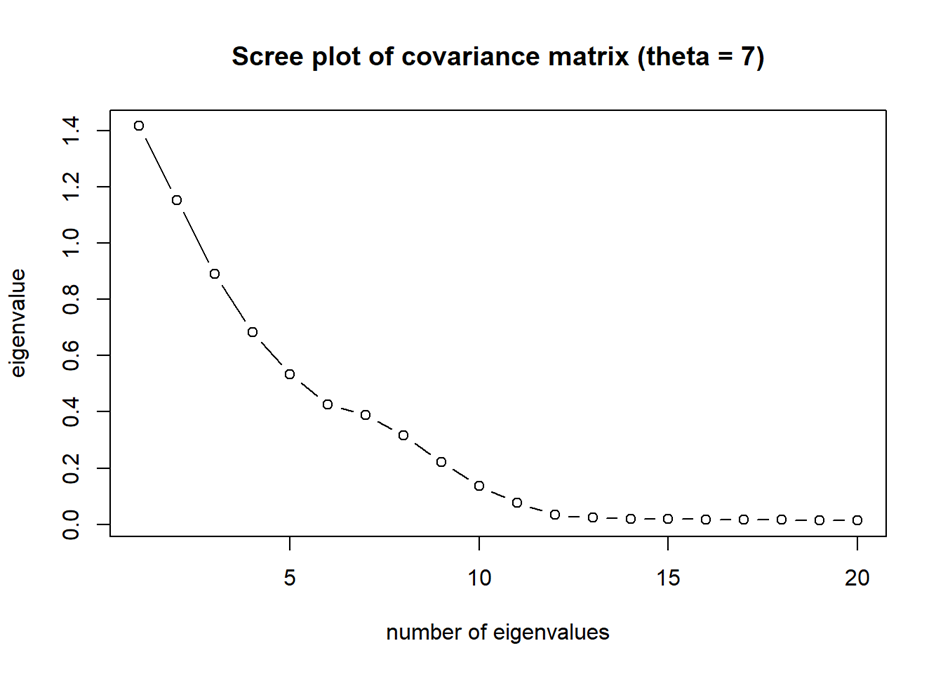

Source: Kris Boudt (R/Finance 2022 presentation)
A solution is to do exploit the information about the comovement as revealed in the higher order moments. The paper by Lu, Huang and Boudt introduces the approach of doing PCA on the cross-products in the third-order covariation as collected in the matrix C = XT ((XXT ) ∘ (XXT ))X, with ∘ the Hadamard product. This is a square matrix for which the eigenvalues are mostly determined by the common factors. A screeplot of the eigenvalues of C thus provides insight on the number of factors. In the simulated weak factor case, they then obtain the following the plot:
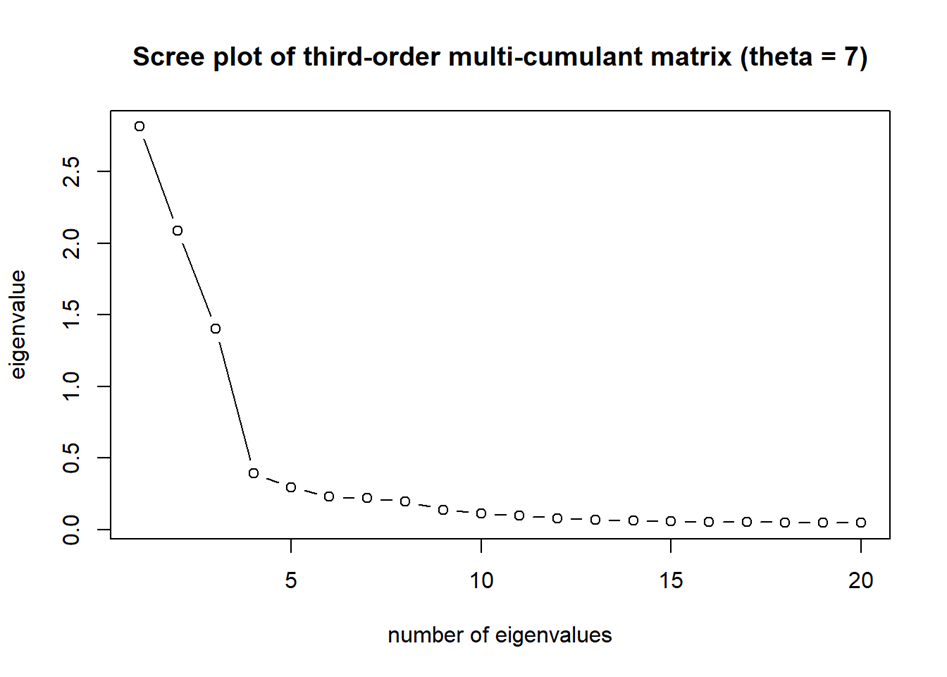

Source: Kris Boudt (R/Finance 2022 presentation)
Since the eigenvalues that correspond to the factors are much larger than those that correspond to the error variation, one can estimate the number of factors as the one that maximizes the ratio of two subsequent eigenvalues in the scree plot. Once you know the number of factors, you can estimate the loadings as the eigenvectors of the matrix C. Given those loadings, the factors are then proportional to the product of the data-matrix X with those loadings.
The method offers the highest gains compared to standard PCA when you have non-normal factors and normal errors, and when factors are weak. The empirical gains are of course case specific. In their application, the authors find significant mean squared prediction error gains when forecasting the equity market premium over the period 1985-2018.
Are you interested to test this methodology on your data? The good news is that this is easy to do. The authors have released their code in the open source R package hofa and have also released several vignettes explaining the method.
Installing the developer version of the hofa package is possible by:
devtools::install_github("GuanglinHuang/hofa")The number of non-Gaussian factors is obtained using the M3.select function:
hofa::M3.select(X, method = "GER3")The factors and factor loadings are obtained using the M3.als function:
hofa::M3.als(X)Link to the hofa package: https://github.com/GuanglinHuang/hofa and https://rpubs.com/guanglin/876536
Link to the R/Finance slides: https://tinyurl.com/slidesHFA
Link to the paper: https://ssrn.com/abstract=3599632
Visit www.sentometrics.com to learn more about this topic.
Disclosure: Interactive Brokers
Information posted on IBKR Campus that is provided by third-parties does NOT constitute a recommendation that you should contract for the services of that third party. Third-party participants who contribute to IBKR Campus are independent of Interactive Brokers and Interactive Brokers does not make any representations or warranties concerning the services offered, their past or future performance, or the accuracy of the information provided by the third party. Past performance is no guarantee of future results.
This material is from Sentometrics and is being posted with its permission. The views expressed in this material are solely those of the author and/or Sentometrics and Interactive Brokers is not endorsing or recommending any investment or trading discussed in the material. This material is not and should not be construed as an offer to buy or sell any security. It should not be construed as research or investment advice or a recommendation to buy, sell or hold any security or commodity. This material does not and is not intended to take into account the particular financial conditions, investment objectives or requirements of individual customers. Before acting on this material, you should consider whether it is suitable for your particular circumstances and, as necessary, seek professional advice.