Guide to Fuzzy Matching with Python

This post is going to delve into the textdistance package in Python, which provides a large collection of algorithms to do fuzzy matching.

The textdistance package

Similar to the stringdist package in R, the textdistance package provides a collection of algorithms that can be used for fuzzy matching. To install textdistance using just the pure Python implementations of the algorithms, you can use pip like below:

pip install textdistance

However, if you want to get the best possible speed out of the algorithms, you can tweak the pip install command like this:

pip install textdistance[extras]

Once installed, we can import textdistance like below:

import textdistance

Levenshtein distance

Levenshtein distance measures the minimum number of insertions, deletions, and substitutions required to change one string into another. This can be a useful measure to use if you think that the differences between two strings are equally likely to occur at any point in the strings. It’s also more useful if you do not suspect full words in the strings are rearranged from each other (see Jaccard similarity or cosine similarity a little further down).

textdistance.levenshtein("this test", "that test") # 2
 
textdistance.levenshtein("test this", "this test") # 6

Jaro-Winkler

Jaro-Winkler is another similarity measure between two strings. This algorithm penalizes differences in strings more earlier in the string. A motivational idea behind using this algorithm is that typos are generally more likely to occur later in the string, rather than at the beginning. When comparing “this test” vs. “test this”, even though the strings contain the exact same words (just in different order), the similarity score is just 2/3. If it matters more that the beginning of two strings in your case are the same, then this could be a useful algorithm to try.

textdistance.jaro_winkler("this test", "test this") # .666666666...

Jaccard Similarity

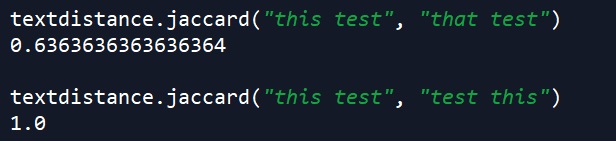
Jaccard similarity measures the shared characters between two strings, regardless of order. In the first example below, we see the first string, “this test”, has nine characters (including the space). The second string, “that test”, has an additional two characters that the first string does not (the “at” in “that”). This measure takes the number of shared characters (seven) divided by this total number of characters (9 + 2 = 11). Thus, 7 / 11 = .636363636363…

In the second example, the strings contain exactly the same characters, just in a different order. Thus, since order doesn’t matter, their Jaccard similarity is a perfect 1.0.

textdistance.jaccard("this test", "that test")
 
textdistance.jaccard("this test", "test this")

Cosine similarity

Cosine similarity is a common way of comparing two strings. This algorithm treats strings as vectors, and calculates the cosine between them. Similar to Jaccard Similarity from above, cosine similarity also disregards order in the strings being compared.

For example, here we compare the word “apple” with a rearranged anagram of itself. This gives us a perfect cosine similarity score.

textdistance.cosine("apple", "ppale") # 1.0

On the other hand, we get the below result when comparing our two example strings that have slightly different characters. Since the calculation behind cosine similarity differs a bit from Jaccard Similarity, the results we get when using each algorithm on two strings that are not anagrams of each other will be different i.e. we’ll get the same perfect result from each algorithm when comparing two strings that are just rearranged variations of each other, but for other cases, the algorithms will generally return different numeric results.

textdistance.cosine("this test", "that test")

Needleman-Wunsch

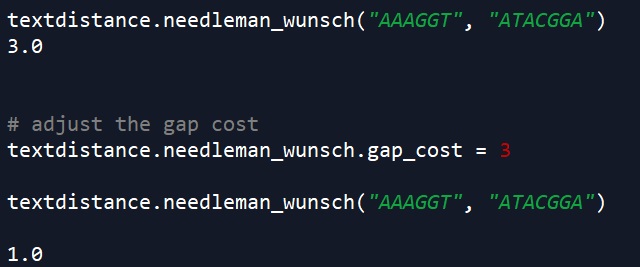
Needleman-Wunsch is often used in bioinformatics to measure similarity between DNA sequences. In effect, it tries to adjust one string (e.g. a string representing DNA) to line up with another string (e.g. of DNA). This algorithm has a parameter called “gap cost”, which can be adjusted like below. For more information, see this previous post.

textdistance.needleman_wunsch("AAAGGT", "ATACGGA")
 
# adjust the gap cost
textdistance.needleman_wunsch.gap_cost = 3
 
textdistance.needleman_wunsch("AAAGGT", "ATACGGA")

MRA (Match Rating Approach)

The MRA (Match Rating Approach) algorithm is a type of phonetic matching algorithm i.e. it attempts to measure the similarity between two strings based upon their sounds. This algorithm could be useful if you’re handling common misspellings (without much loss in pronunciation), or words that sound the same but are spelled differently (homophones). It was originally developed to compare similar-sounding names. For example, below we compare “tie” and “tye”. The score that gets returned needs to be compared to a mapping table based upon the length of the strings involved (see this link for more detailed information).

textdistance.mra("tie", "tye") # 1

More on textdistance

As a default for certain algorithms, textdistance (when installed with extras) will try to find external libraries when a function is called. The purpose behind this is try get the implementation with optimal speed. This can be turned off like below.

textdistance.jaro_winkler.external = False
 
textdistance.jaro_winkler("second test", "2nd test")

That’s it for this post! In conclusion, it’s important to assess your use case when doing fuzzy matching since there’s quite a few algorithms out there. It can be useful to experiment with a few of them for your problem to test out which one works best.

Hope you enjoyed reading a guide to fuzzy matching with Python! 

Originally posted on TheAutomatic.net Blog.