How to Create Kalman Filter in Python – Part IV

See Part I, Part II and  Part III of this series to get started with the Statistical terms and concepts used in Kalman Filter.

Kalman Gain equation

Recall that we talked about the normal distribution in the initial part of this blog. Now, we can say that the errors, whether measurement or process, are random and normally distributed in nature. In fact, taking it further, there is a higher chance that the estimated values will be within one standard deviation from the actual value.

Now, Kalman gain is a term which talks about the uncertainty of the error in the estimate. Put it simply, we denote ρ as the estimate uncertainty.

Since we use σ as the standard deviation, we would denote the variance of the measurement σ² due to the uncertainty as ⋎. Thus, we can write the Kalman Gain as,

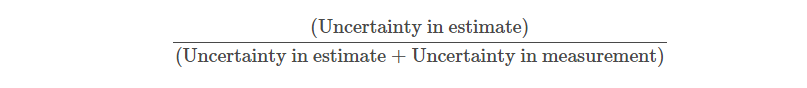
In the Kalman filter, the Kalman gain can be used to change the estimate depending on the estimate measure.

Since we saw the computation of the Kalman gain, in the next equation we will understand how to update the estimate uncertainty.

Before we move to the next equation in the Kalman filter tutorial, we will see the concepts we have gone through so far. We first looked at the state update equation which is the main equation of the Kalman filter. We further understood how we extrapolate the current estimated value to the anticipated value which becomes the current estimate in the next step. The third equation is the Kalman gain equation which tells us how the uncertainty in the error plays a role in calculating the Kalman gain. Now we will see how we update the Kalman gain in the Kalman filter equation. Let’s move on to the fourth equation in the Kalman filter tutorial.

Stay tuned for the next installment, in which the Rekhit will estimate uncertainty update and extrapolation.

Download the full code: https://blog.quantinsti.com/kalman-filter/.

All data and information provided in this article are for informational purposes only. QuantInsti® makes no representations as to accuracy, completeness, currentness, suitability, or validity of any information in this article and will not be liable for any errors, omissions, or delays in this information or any losses, injuries, or damages arising from its display or use. All information is provided on an as-is basis.