Optimal Trading with a Trailing Stop

The recent market turbulence has led to high volatility and large drawdown in equity prices. It’s more important than ever to incorporate risk management tools into trading systems to avert significant losses. 

Trailing stops are popular trade orders widely used by proprietary traders and retail investors to provide downside protection. In contrast to a stop-loss exit which closes a position at a fixed price, a trailing stop is characterized by a stochastic floor that moves based on the running maximum of the asset price. This provides a dynamic downside protection as the stochastic floor is automatically adjusted upward whenever the asset price moves to a new high. 

A trailing stop is triggered when the prevailing price of an asset falls below the stochastic floor. The asset price at the trailing stop may be higher than its starting price. 

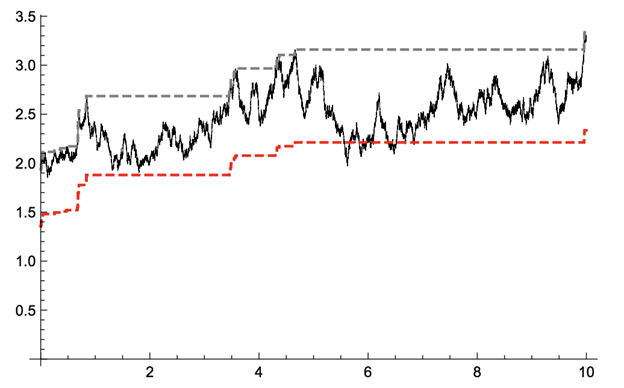
Sample paths of the asset price (solid black), its running maximum (gray dashed), and the 30%- drawdown floor representing the trailing stop (red dashed).
Source: Leung and Zhang (2021) 

In essence, a trailing stop allows an investor to specify a limit on the maximum possible loss while not limiting the maximum possible gain. This is particularly relevant in common trend-following strategies, and trailing stop provides an automatic trigger to exit when prices start to trend downward due to, for example, regime switching. 

In addition to setting a trailing stop order, the investor can also use a limit order to sell at a certain price target. If the price is sufficiently high, the investor may prefer to take profit immediately, rather than waiting further with the possibility of setting off the trailing stop. The investor’s position will be liquidated by either order, whichever comes first. 

This gives rise to an interesting and challenging problem: what is the best timing strategy to liquidate a position subject to a trailing stop? Mathematically, we recognize the trailing stop as a stochastic timing constraint in the sense that it installs a path-dependent random maturity (as opposed to selling at a fixed time) into the liquidation problem, rendering the problem significantly more difficult to analyze or solve. Furthermore, the investor can decide when to establish the position in the first place. This leads us to also analyze the optimal timing to enter the market. 

In Leung & Zhang (2021) we analyze an optimal double timing problem (for entry & exit) subject to a trailing stop. Using the excursion theory of linear diffusion, we derive the mathematically optimal strategy and discuss the effect of trailing stopping on the optimal trading strategies analytically and numerically. Our method of solution applies to a general class of stochastic models for stock prices, and our analytical results facilitate computation of the optimal timing strategies. 

Among our results, we show that it is optimal to use a limit sell order at a sufficiently high price. In other words, once the investor enters the market, he/she can immediately set the optimal limit sell order together with the trailing stop order, and wait for either order to be executed automatically. 

Incorporating trailing stops may lead to nontrivial and possibly quite consequential effects to a trading system. For further discussion on this topic and research collaboration, reach out via email or check out the CFRM Quantitative Analytics Lab. 

Links: Tim Leung’s Google Scholar // Linkedin Page // Homepage 

Disclaimer: This post is not intended to be investment advice. 

References 

T. Leung and H. Zhang (2021), Optimal Trading with a Trailing Stop, Applied Math & Optimization, 83, pages 669–698 [pdf;link] 

H. Zhang (2019), Stochastic Drawdowns, Modern Trends in Financial Engineering: Volume 2, World Scientific [link] 

T. Leung T. and X. Li (2016), Optimal mean reversion trading: mathematical analysis and practical applications, World Scientific Publishing Co. [link] 

T. Leung T. and X. Li (2015), Optimal Mean Reversion Trading with Transaction Costs & Stop-Loss Exit, International Journal of Theoretical & Applied Finance, vol 18, issue 3, p.1550020 [link]