Really Large Numbers in R

This post will discuss ways of handling huge numbers in R using the gmp package.

The gmp package

The gmp package provides us a way of dealing with really large numbers in R. For example, let’s suppose we want to multiple 10²⁵⁰ by itself. Mathematically we know the result should be 10⁵⁰⁰. But if we try this calculation in base R we get Inf for infinity.

num = 10^250
 
num^2 # Inf

However, we can get around this using the gmp package. Here, we can convert the integer 10 to an object of the bigz class. This is an implementation that allows us to handle very large numbers. Once we convert an integer to a bigz object, we can use it to perform calculations with regular numbers in R (there’s a small caveat coming).

library(gmp)
 
num = as.bigz(10)
 
(num^250) * (num^250)
 
# or directly 10^500
num^500

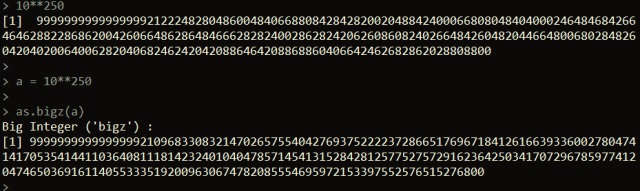
One note that we need to be careful about is what numbers we use to convert to bigz objects. In the example above, we convert the integer 10 to bigz. This works fine for our calculations because 10 is not a very large number in itself. However, let’s suppose we had converted 10²⁵⁰ to a bigz object instead. If we do this, the number 10²⁵⁰ becomes a double data type, which causes a loss in precision for such a number. Thus the result we see below isn’t really 10²⁵⁰:

num = 10^250
 
as.bigz(num)
 
num

A way around this is to input the number we want as a character into as.bigz. For example, we know that 10²⁵⁰ is the number 1 followed by 250 zeros. We can create a character that represents this number like below:

num = paste0("1", paste(rep("0", 250), collapse = ""))

Thus, we can use this idea to create bigz objects:

as.bigz(num)

In case you run into issues with the above line returning an NA value, you might want to try turning scientific notation off. You can do that using the base options command.

options(scipen = 999)

If scientific notation is not turned off, you may have cases where the character version of the number looks like below, which results in an NA being returned by as.bigz.

“1e250”

In general, numbers can be input to gmp functions as characters to avoid this or other precision issues.

Finding the next prime

The gmp package can find the first prime larger than an input number using the nextprime function.

num = "100000000000000000000000000000000000000000000000000"
 
nextprime(num)

Find the GCD of two huge numbers

We can find the GCD of two large numbers using the gcd function:

num = "2452345345234123123178"
num2 = "23459023850983290589042"
 
gcd(num, num2) # returns 2

Factoring numbers into primes

gmp also provides a way to factor numbers into primes. We can do this using the factorize function.

num = "2452345345234123123178"
 
factorize(num)

Matrices of large numbers

gmp also supports creating matrices with bigz objects.

num1 <- "1000000000000000000000000000"
num2 <- "10000000000000000000000000000000"
num3 <- "100000000000000000000000000000000000000"
num4 <- "100000000000000000000000000000000000000000000000"
 
nums <- c(as.bigz(num1), as.bigz(num2), as.bigz(num3), as.bigz(num4))
 
matrix(nums, nrow = 2)

We can also perform typical operations with our matrix, like find its inverse, using base R functions:

solve(m)

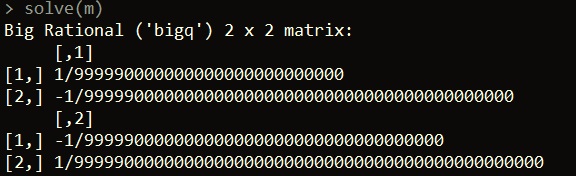
Sampling random (large) numbers uniformly

We can sample large numbers from a discrete uniform distribution using the urand.bigz function.

urand.bigz(nb = 100, size = 5000, seed = 0)

The nb parameter represents how many integers we want to sample. Thus, in this example, we’ll get 100 integers returned. size = 5000 tells the function to sample the integers from the inclusive range of 0 to 2⁵⁰⁰⁰ – 1. In general you can sample from the range 0 to 2^size – 1.

To learn more about gmp, click here for its vignette.

Originally posted on the TheAutomatic.net Blog.

Disclosure: Interactive Brokers

Information posted on IBKR Campus that is provided by third-parties and not by Interactive Brokers does NOT constitute a recommendation by Interactive Brokers that you should contract for the services of that third party. Third-party participants who contribute to IBKR Campus are independent of Interactive Brokers and Interactive Brokers does not make any representations or warranties concerning the services offered, their past or future performance, or the accuracy of the information provided by the third party. Past performance is no guarantee of future results.

This material is from TheAutomatic.net and is being posted with permission from TheAutomatic.net. The views expressed in this material are solely those of the author and/or TheAutomatic.net and IBKR is not endorsing or recommending any investment or trading discussed in the material. This material is not and should not be construed as an offer to sell or the solicitation of an offer to buy any security. To the extent that this material discusses general market activity, industry or sector trends or other broad based economic or political conditions, it should not be construed as research or investment advice. To the extent that it includes references to specific securities, commodities, currencies, or other instruments, those references do not constitute a recommendation to buy, sell or hold such security. This material does not and is not intended to take into account the particular financial conditions, investment objectives or requirements of individual customers. Before acting on this material, you should consider whether it is suitable for your particular circumstances and, as necessary, seek professional advice.

In accordance with EU regulation: The statements in this document shall not be considered as an objective or independent explanation of the matters. Please note that this document (a) has not been prepared in accordance with legal requirements designed to promote the independence of investment research, and (b) is not subject to any prohibition on dealing ahead of the dissemination or publication of investment research.

Any trading symbols displayed are for illustrative purposes only and are not intended to portray recommendations.