Kalman Filter Python: Tutorial and Strategies – Part II

Learn about the applications of Kalman filter in trading with Part I.

Kalman filter equations

Kalman Filter is a type of prediction algorithm. Thus, the Kalman filter’s success depends on our estimated values and its variance from the actual values. In the Kalman filter, we assume that depending on the previous state, we can predict the next state.

At the outset, we would like to clarify that this Kalman Filter tutorial is not about the derivation of the equations but trying to explain how the equations help us in estimating or predicting a value.

Now, as we said earlier, we are trying to predict the value of something which cannot be directly measured. Thus, there will obviously be some error in the predicted value and the actual value.

• If the system itself contains some errors, then it is called measurement noise.
  For example, if the weighing scale itself shows different readings for the same football player, it will be measurement noise.
• If the process when the measurement takes place has certain factors which are not taken into account, then it is called process noise.
  For example, if we are predicting the Apollo Rocket’s position, and we could not account for the wind during the initial blast off phase, then we will encounter some error between the actual location and the predicted location.

Kalman Filter is used to reduce these errors and successfully predict the next state.

Now, suppose we pick out one player and weigh that individual 10 times, we might get different values due to some measurement errors.

Mr. Rudolf Kalman developed the status update equation taking into account three values, i.e.

• True value
• The estimated or predicted value
• Measured value

Status update equation

The status update equation is as follows:

Current state estimated value
= Predicted value of current state + Kalman Gain * ( measured value – predicted value of the state)

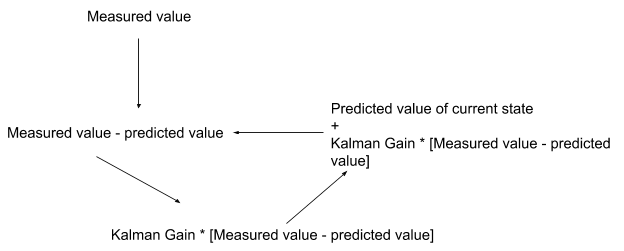
Let us understand this equation further.

In our example, we can say that given the measured values of all ten measurements, we will take the average of the values to estimate the true value.

To work this equation, we take one measurement which becomes the measured value. In the initial step, we guess the predicted value.

Now since the average is computed, in this example, the Kalman gain would be (1/N) as with each successive iteration, the second part of the equation would be decreasing, thus giving us a better-estimated value.

We should note that the current estimated value becomes the predicted value of the current state in the next iteration.

For now, we know that the actual weight is constant, and hence it was easy to predict the estimated value. But what if we had to take into account that the state of the system (which was the weight in this case) changes?

For that, we will now move on to the next equation in the Kalman Filter tutorial i.e. State extrapolation.

State extrapolation equation

The state extrapolation system helps us to find the relation between the current state and the next state i.e. predict the next state of the system.

Until now, we understood that the Kalman filter is recursive in nature and uses the previous values to predict the next value in a system. While we can easily give the formula and be done with it, we want to understand exactly why it is used. In that respect, we will take another example to illustrate the state extrapolation equation.

Now, let’s take the example of a company trying to develop a robotic bike. If you think about it, when someone is riding a bike, they have to balance the bike, control the accelerator, turn etc.

Let’s say that we have a straight road and we have to control the bike’s velocity. For this, we would have to know the bike’s position. As a simple case, we measure the wheels’ rotation to predict how much the bike has moved. We remember that the distance travelled by an object is equal to the velocity of the object multiplied by the time travelled.

Now, Let’s suppose we measure the rotation at a certain instant of time, ie Δt.

If we say that the bike has a constant velocity v, then we can say the following:

The predicted position of the bike is equal to the current estimated position of the bike + the distance covered by the bike in time Δt.

Here the distance covered by the bike will be the result of Δt multiplied by the velocity of the bike.

Suppose that the velocity is kept constant at 2 m/s. And the time Δt is 5 seconds. That means the bike moves 10 metres between every successive measurement.

But what if we check the next time and find out the bike moved 12 metres? This gives us an error of 2 metres. This could mean two things,

1. The device used to measure the velocity has an error (measurement error)
2. The bike is moving at different velocities, in this instance maybe it is a downhill slope (process error)

We try to find out how to minimise this error by having different gains to apply to the state update equation.

Now, we will introduce a new concept to the Kalman filter tutorial, i.e. the α – β filter.

Now, if we recall the status update equation, it was given as,

Current state estimated value
= Predicted value of current state + Kalman Gain * ( measured value – predicted value of the state)

We will say that α is used to reduce the error in the measurement, and thus it will be used to predict the value of the position of the object.

Now if we keep the α in place of the Kalman gain, you can deduce that a high value of α gives more importance to the measured value and a low level of α gives less weightage to the measured value. In this way, we can reduce the error while predicting the position.

Now, if we assume that the bike is moving with different velocities, we would have to use another equation to compute the velocity and which in turn would lead to a better prediction to the position of the bike. Here we use β in place of Kalman gain to estimate the velocity of the bike.

We tried to see the relation of how α and β impact the predicted value. But how do we know for sure the correct value of α and β in order to get the predicted value closer to the actual value?

Let us move on to the next equation in the Kalman filter tutorial, i.e. the Kalman Gain equation.

Kalman gain equation

Recall that we talked about the normal distribution in the initial part of this blog. Now, we can say that the errors, whether measurement or process, are random and normally distributed in nature. In fact, taking it further, there is a higher chance that the estimated values will be within one standard deviation from the actual value.

Now, Kalman gain is a term which talks about the uncertainty of the error in the estimate. Put simply, we denote ρ as the estimated uncertainty.

Since we use σ as the standard deviation, we would denote the variance of the measurement σ2 due to the uncertainty as ⋎.

Thus, we can write the Kalman Gain as,

(Uncertainty in estimate)

(Uncertainty in estimate + Uncertainty in measurement)

(Uncertainty in estimate)(Uncertainty in estimate + Uncertainty in measurement)

In the Kalman filter, the Kalman gain can be used to change the estimate depending on the estimated measure.

Since we saw the computation of the Kalman gain, in the next equation we will understand how to update the estimated uncertainty.

Before we move to the next equation in the Kalman filter tutorial, we will see the concepts we have gone through so far. We first looked at the state update equation which is the main equation of the Kalman filter.

We further understood how we extrapolate the current estimated value to the predicted value which becomes the current estimate in the next step. The third equation is the Kalman gain equation which tells us how the uncertainty in the error plays a role in calculating the Kalman gain.

Now we will see how we update the Kalman gain in the Kalman filter equation.

Let’s move on to the fourth equation in the Kalman filter tutorial.

Estimate uncertainty update

In the Kalman Filter tutorial, we saw that the Kalman gain was dependent on the uncertainty in the estimation. Now, as we know with every successive step, the Kalman Filter continuously updates the predicted value so that we get the estimated value as close to the actual value of a variable, thus, we have to see how this uncertainty in the error can be reduced.

While the derivation of the equation is lengthy, we are only concerned about the equation.

Thus, the estimate uncertainty update equation tells us that the estimated uncertainty of the current state varies from the previous estimate uncertainty by the factor of (1 – Kalman gain). We can also call this the covariance update equation.

This brings us to the last equation of the Kalman filter tutorial, which we will see below.

Estimate uncertainty extrapolation

The reason why the Kalman filter is popular is because it continuously updates its state depending on the predicted and measured current value. Recall that in the second equation, we had extrapolated the state of the estimate. Similarly, the estimated uncertainty of the current error is used to predict the uncertainty of the error in the next state.

Ok. That was simple!

This was a no equation way to describe the Kalman filter. If you are confused, let us go through the process and see what we have learned so far.

For input, we have measured value. Initially, we use certain parameters for the Kalman gain as well as the predicted value. We will also make a note of the estimated uncertainty.

Now we use the Kalman filter equation to find the next predicted value.

In the next iteration, depending on how accurate our predicted variable was, we make changes to the uncertainty estimate which in turn would modify our Kalman gain.

Thus, we get a new predicted value which will be used as our current estimate in the next phase.

In this way, with each step, we would get closer to predicting the actual value with a reasonable amount of success.

That is all there is to it. We would reiterate in this Kalman filter tutorial that the reason the Kalman filter is popular is because it only needs the previous value as input and depending on the uncertainty in the measurement, the resulting value is predicted.

In the real world, the Kalman filter is used by implementing matrix operations as the complexity increases when we take real-world situations. If you are interested in the maths part of the Kalman filter, you can go through this resource to find many examples illustrating the individual equations of the Kalman filter.

Moving forward, we will see the comparison of Kalman filter with other filtering techniques to make the topic more clear.

---

Kalman filter and other filtering techniques

Let us dive into the differences between Kalman filtering and other filtering techniques on the basis of advantages, disadvantages and applicability of each technique. ⁽³⁾

Filtering Technique	Advantages	Disadvantages	Applicability
Kalman Filter	Optimal under Gaussian noise assumptions. Efficient for linear systems. Provides estimates of state and error covariance.	Assumes linearity and Gaussian noise, which may not hold in all cases. Can be computationally expensive for high-dimensional systems.	Tracking moving averages in trading algorithms. Predicting future price movements based on historical data.
Extended Kalman Filter (EKF)	Allows for nonlinear system models by linearizing them via Taylor series expansion. More flexible than the standard Kalman filter.	Linearization introduces approximation errors, leading to suboptimal performance in highly nonlinear systems. May suffer from divergence issues if the linearization is inaccurate.	Modelling complex trading strategies involving non-linear relationships between market variables.
Unscented Kalman Filter (UKF)	Avoids linearization by propagating a set of sigma points through the nonlinear functions. More accurate than EKF for highly nonlinear systems. Better performance with non-Gaussian noise.	Requires tuning parameters for the selection of sigma points, which can be challenging. May suffer from sigma point degeneracy in high-dimensional spaces.	Estimating the state of a financial market model with highly nonlinear dynamics.
Particle Filter (Sequential Monte Carlo)	Handles nonlinear and non-Gaussian systems without requiring linearisation. Robust to multimodal distributions. Can represent complex distributions with particles.	Computational complexity increases with the number of particles, making it less efficient for high-dimensional state spaces. Sampling inefficiency can lead to particle degeneracy and sample impoverishment.	Tracking multiple potential market scenarios simultaneously, such as predicting the movement of various assets in a portfolio.
Complementary Filter	Simple to implement and computationally efficient. Effective for fusing data from multiple sensors with complementary characteristics.	Requires manual tuning of sensor fusion parameters, which may not be optimal in all situations. Limited applicability to systems with highly correlated sensor errors.	Combining technical indicators, such as moving averages and momentum oscillators, to generate trading signals.

When it comes to trading, the Kalman filter forms an important component in the pairs trading strategy. Let us build a simple pairs trading strategy using the Kalman Filter in Python now.

Author: Chainika Thakar (Originally written by Rekhit Pachanekar)

Stay tuned to learn about implementing Kalman filter in Python

Originally posted on QuantInsti blog.