Central Limit Theorem explained in Python (with examples)

The Central Limit Theorem (CLT) is often referred to as one of the most important theorems, not only in statistics but also in the sciences as a whole. In this blog, we will try to understand the essence of the Central Limit Theorem with simulations in Python.

Samples and the Sampling Distribution

Before we get to the theorem itself, it is first essential to understand the building blocks and the context. The main goal of inferential statistics is to draw inferences about a given population, using only its subset, which is called the sample. We do so because generally, the parameters which define the distribution of the population, such as the population mean μ and the population variance σ², are not known.

In such situations, a sample is typically collected in a random fashion, and the information gathered from it is then used to derive estimates for the entire population.

The above-mentioned approach is both time-efficient and cost-effective for the organization/firm/researcher conducting the analysis. It is important that the sample is a good representation of the population, in order to generalize the inferences drawn from the sample to the population in any meaningful way.

The challenge though is that being a subset, the sample estimates are well, just estimates, and hence prone to error! That is, they may not reflect the population accurately. For example, if we are trying to estimate the population mean (μ) using a sample mean , then depending on which observations land in the sample, we might get different estimates of the population with varying levels of errors.

---

What is the Central Limit Theorem?

The core point here is that the sample mean itself is a random variable, which is dependent on the sample observations. Like any other random variable in statistics, the sample mean also has a probability distribution, which shows the probability densities for different values of the sample mean.

This distribution is often referred to as the ‘sampling distribution’. The following diagram summarizes this point visually:

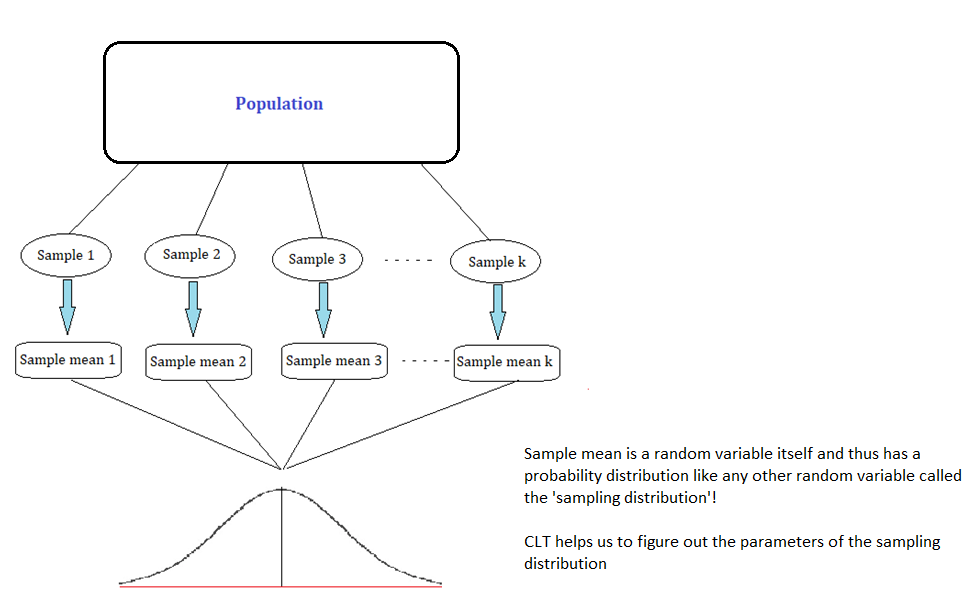
The Central Limit Theorem essentially is a statement about the nature of the sampling distribution of the sample mean under some specific condition, which we will discuss in the next section.

Stay tuned for the next installment, in which Ashutosh Dave will discuss Central Limit Theorem: Statement & Assumptions.

Visit QuantInsti for additional details and to download full code: https://blog.quantinsti.com/central-limit-theorem/.

Disclaimer: All investments and trading in the stock market involve risk. Any decisions to place trades in the financial markets, including trading in stock or options or other financial instruments is a personal decision that should only be made after thorough research, including a personal risk and financial assessment and the engagement of professional assistance to the extent you believe necessary. The trading strategies or related information mentioned in this article is for informational purposes only.