Trading decisions often depend on the trader’s subjective belief of the distribution of the asset price on a given future date. For example, if a trader anticipates a big price movement for a company stock after its earnings announcement, then perhaps a long straddle position makes sense. There are many instances like this. And as time progresses, the trader will learn more about the price distribution by observing price fluctuations.
Mathematically, the trader’s market view can be described by a prior distribution of the asset price on some future date. The price process reveals itself over time, but there is also uninformative noise embedded in the asset price dynamics. This leads to the question: how to build a stochastic model that appropriately reflects the trader’s market view dynamically over time?
A randomized Brownian bridge is the perfect candidate for this. In our recent paper, we present a randomized Brownian bridge (rBb) model, whereby the log-price of the asset follows a Brownian bridge with a randomized endpoint representing the random terminal log-price.
The trader’s belief is described by a real-valued random variable D to be realized at some future time T so that the terminal log-price of the asset is given by
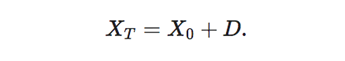
In turn, the log-price process admits the following form
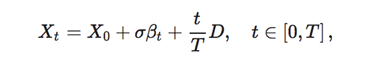
where
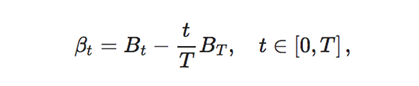
is a standard Brownian bridge. Exponentiating the log-price recovers the underlying asset price process.
To utilize our model, the trader would specify a distribution for the stock price at some future time (e.g. end of the month, option expiration date, earnings announcement date). In contrast to almost all existing models, the trader here has total freedom in choosing any future marginal distribution as desired. It can be as simple as a two-point discrete distribution, the normal distribution, or other more sophisticated distributions.
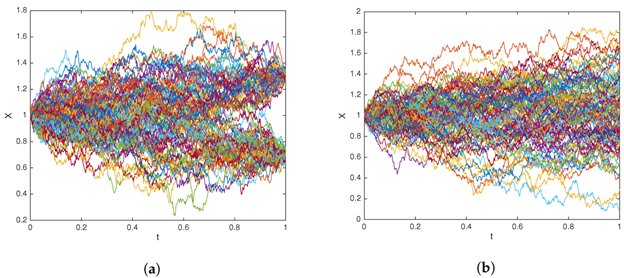
Path simulation of a randomized Brownian bridge, representing the log-price of the stock, with the prior belief on the terminal log-price following (a) two-point discrete distribution and (b) normal distribution. Note how the paths tend to converge to match the pre-specified distribution. Source: Leung et al (2018) (see Reference below)
Through a Bayesian approach with some stochastic calculus, the trader’s prior belief and learning mechanism can be encoded in the drift of the log-price process. One can also compute the statistics associated with the price process.
In the same paper, we introduce an optimal stopping approach to the trader’s liquidation problem, which is applicable not only to selling the underlying asset, but also options written on it. To solve the trader’s optimal stopping problem, we devise and apply a number of analytical tools.
We introduce the optimal liquidation premium which represents the additional value from optimally waiting to sell, as opposed to immediate liquidation. Indeed, as soon as this premium vanishes, it is optimal for the trader to sell. On the other hand, if this premium is always strictly positive, then the trader finds it optimal to wait through maturity. Therefore, the optimal liquidation premium provides not only new financial interpretations, but also another avenue of analytical investigation of the optimal stopping problem.
Among our results, we identify the conditions under which it is optimal to immediately liquidate, or hold the asset/option position through expiration. Furthermore, we derive the variational inequality associated with the optimal stopping problems, and present a finite-difference method to solve for the optimal trading boundaries. The optimal trading strategies are solved numerically and compared across different prior beliefs.
Reference
T. Leung, J. Li, and X. Li, Optimal Timing to Trade Along a Randomized Brownian Bridge [link], International Journal of Financial Studies, 6(3),75, pp.1–23, 2018
Disclosure: Interactive Brokers
Information posted on IBKR Campus that is provided by third-parties does NOT constitute a recommendation that you should contract for the services of that third party. Third-party participants who contribute to IBKR Campus are independent of Interactive Brokers and Interactive Brokers does not make any representations or warranties concerning the services offered, their past or future performance, or the accuracy of the information provided by the third party. Past performance is no guarantee of future results.
This material is from Computational Finance & Risk Management, University of Washington and is being posted with its permission. The views expressed in this material are solely those of the author and/or Computational Finance & Risk Management, University of Washington and Interactive Brokers is not endorsing or recommending any investment or trading discussed in the material. This material is not and should not be construed as an offer to buy or sell any security. It should not be construed as research or investment advice or a recommendation to buy, sell or hold any security or commodity. This material does not and is not intended to take into account the particular financial conditions, investment objectives or requirements of individual customers. Before acting on this material, you should consider whether it is suitable for your particular circumstances and, as necessary, seek professional advice.
Disclosure: Options Trading
Options involve risk and are not suitable for all investors. Multiple leg strategies, including spreads, will incur multiple commission charges. For more information read the "Characteristics and Risks of Standardized Options" also known as the options disclosure document (ODD) or visit ibkr.com/occ