Grokking Linear Regression Analysis in Finance – Part IV

See Part I, Part II and Part III for an overview of the linear models and a detailed look at multiple linear regression.

Linear Regression of a Non-linear Relationship

Suppose we have a model like so:

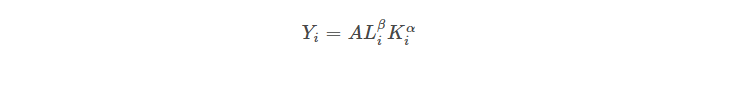
For the curious reader, this is the Cobb-Douglas production function, where

• Y_i – Total production in the i^th economy
• L – Labor input in the i^th economy
• K – Capital input in the i^th economy
• A – Total factor productivity

We can linearize it by taking logarithms on both sides to get

log Y_i = log A + β log L_i + α log K_i

This is still a multiple linear regression equation.

Since the coefficients α and β are linear (i.e. they have degree 1).

We can use standard procedures like the OLS (details below) to estimate them if we have the data for Y, L and K.

Model Parameters and Model Estimates

In equation 1, the values of Y_i and X_i can be easily computed from an OHLC data set for each day. However, that is not the case with β₀, β₁ and ϵ_i. We need to estimate them from the data.

Estimation theory is at the heart of how we do it. We use Ordinary Least Squares (or Maximum Likelihood Estimation) to get a handle on the values of β₀ and β₁. We call the process of finding the best estimates for the model parameters as “fitting” or “training” the model.

Estimates, however, are still estimates. We never know the actual theoretical values of the model parameters (i.e. β₀ and β₁). OLS helps us make a conjecture based on what their values are. The hats we put over them are to denote that they are model estimates.

In quantitative finance, our data sets are small, mostly numerical, and have a low signal-to-noise ratio. Therefore, our parameter estimates have a high margin of error.

So what’s OLS?

OLS is Ordinary Least Squares. It’s an important estimation technique used to estimate the unknown parameters in a linear regression model. I’d earlier mentioned choosing the ‘best’ possible values for the model parameters so that the formula can be as ‘accurate’ as possible. OLS has a particular way of describing ‘best’ and ‘accurate’. Here goes. It estimates the ‘best’ coefficients to be such that we minimize the sum of the squared differences between the predicted values, Ŷ_i (as per the formula) and the actual values, Y_i.

Visit QuantInsti for additional insight on this topic: https://blog.quantinsti.com/linear-regression/.

Disclaimer: All investments and trading in the stock market involve risk. Any decisions to place trades in the financial markets, including trading in stock or options or other financial instruments is a personal decision that should only be made after thorough research, including a personal risk and financial assessment and the engagement of professional assistance to the extent you believe necessary. The trading strategies or related information mentioned in this article is for informational purposes only.

Any trading symbols displayed are for illustrative purposes only and are not intended to portray recommendations.

References

1. Baltagi, Badi H., Econometrics, Springer, 2011.
   
2. Greene, William H., Econometric analysis. Pearson Education, 2018.
   
3. Wooldridge, Jeffrey M., Introductory econometrics: A modern approach, Cengage learning, 2015.