Bond Convexity in Excel and R

A convexity is needed to describe a non-linearity of a bond price, which is absent in a duration. This post explains the meaning and calculation process of the convexity by using Excel and R.

We have calculated a bond duration in the previous post

• Bond Modified Duration in Excel and R

Bond Price

Bond price with unit notional amount, coupon C, YTM y, annual frequency is as follows.

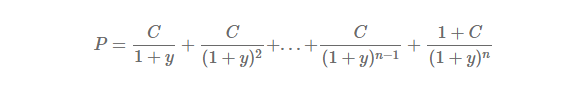
Convexity

As a bond yield decreases, its price rises at an increasing rate, whereas a bond’s price falls at a decreasing rate as its yield increases. This asymmetric behavior is known as convexity. Let’s derive convexity in the same manner by which duration is derived.

At first, the second order derivative of P with respect to y.

Like the duration, factoring out in the above equation yields

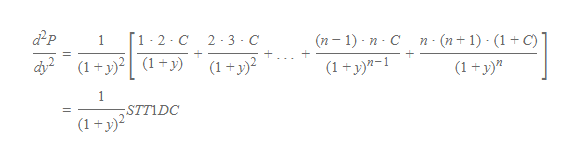
To avoid lengthy expression, we substitute STT1DC for the bracketed term. STT1DC is the abbreviation of the sum of multiplications of time and time + 1 and discounted cash flow (only coupon or coupon + principal amount).

Similar to the duration in the previous post, let’s modify it by a ratio of its initial bond price. Dividing by P gives the following expression for the convexity (C) of a bond.

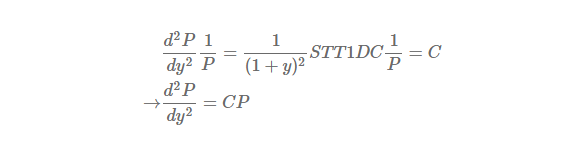
Rearranging this equation, we can get the following expression.

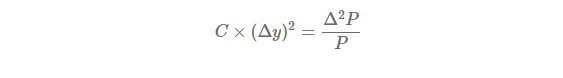
Generalization

When interest conversion period is less than one year such as one quarter, convexity is redefined as follows.

Here, k is the number of compounding periods per year.

Effective Convexity and Duration

Effective convexity (C) is obtained from the numerical differentiation like the effective duration (D).

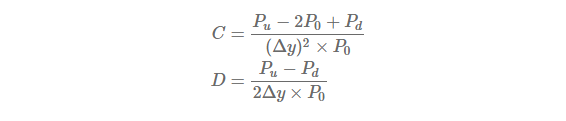
Here, P₀ denotes an initial bond price with yield to maturity (y). P_u and P_d represent bond prices after downward (y − Δy) and upward (y + Δy) shocks to interest rates (yield to maturity) respectively.

Excel Illustration

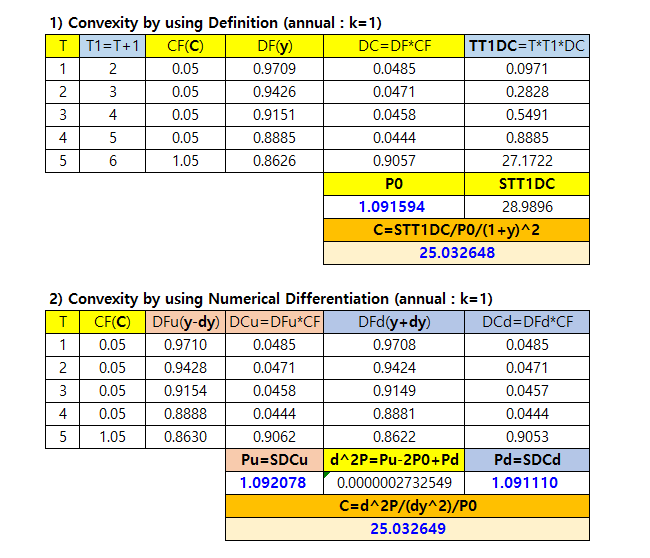
To the best of our knowledge, Excel does not provides a built-in function for the calculation of convexity. Therefore, we calculate convexity by using the definition and the numerical differentiation for our clear understanding. As an example, we use the same specification of bond as in the previous post. Specifically, coupon rate (C), YTM (y), maturity (m), and interest rate change (Δy) are 5%, 3%, 5-year, and 0.0001 (1bp) respectively.

The following Excel spreadsheet shows the case of k=1.

The following Excel spreadsheet shows the case of k=4.

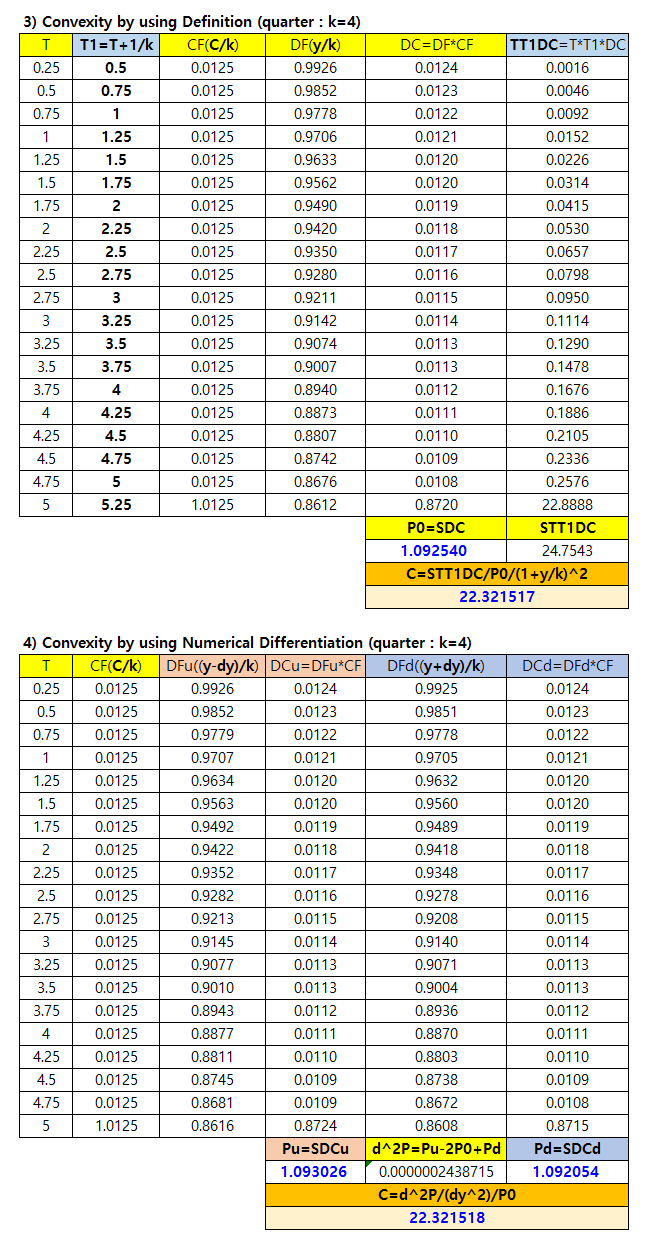
It is worthwhile to note that when k > 1, t + 1 in the convexity definition means t + 1/k.

R code

The following R code use derivmkts R package library which provides functions for the calculations of price, yield, duration, and convexity of a coupon bond. The reason why we use this library is that manual implementation of convexity in R is not very different from the case of the duration in the previous post.

#========================================================#
# Quantitative ALM, Financial Econometrics & Derivatives 
# ML/DL using R, Python, Tensorflow by Sang-Heon Lee 
#
# https://shleeai.blogspot.com
#--------------------------------------------------------#
# Convexity and (modified) Duration
#========================================================#
 
graphics.off()  # clear all graphs
rm(list = ls()) # remove all files from your workspace
 
library(derivmkts) # price, yield, duration, convexity
 
#-------------------------------------------------------
# Input
#-------------------------------------------------------
C   <- 0.05       # coupon rate
y   <- 0.03       # YTM
m   <- 5          # maturity
P   <- 1          # principal amount
cpn <- C*P       # annual coupon amount
 
# k = 1 : coupon payments annually
freq  <- 1
price <- bondpv(cpn, m, y, P, freq)
duration (price, cpn, m, P, freq, modified = TRUE)
convexity(price, cpn, m, P, freq)
 
# k = 4 : coupon payments quarterly
freq  <- 4
price <- bondpv(cpn, m, y, P, freq)
duration (price, cpn, m, P, freq, modified = TRUE)
convexity(price, cpn, m, P, freq)

Running the above R code results in the same output as those of Excel illustration.

> freq  <- 1
> price <- bondpv(cpn, m, y, P, freq)
> duration(price, cpn, m, P, freq, modified = TRUE)
[1] 4.43501
> convexity(price, cpn, m, P, freq)
[1] 25.03265
> 
> freq  <- 4
> price <- bondpv(cpn, m, y, P, freq)
> duration(price, cpn, m, P, freq, modified = TRUE)
[1] 4.450557
> convexity(price, cpn, m, P, freq)
[1] 22.32152
> 

Final Thoughts

From this post, we have understood the meaning of convexity by using an simple derivation and Excel illustration. Finally owing to derivmkt R package, we can easily implement R code for the calculation of convexity not to mention duration and price of a bond. Now we are ready to describes the percent(%) change of bond price more precisely with the help of duration and convexity. This topic will be covered in the next post.

Originally posted on SHLee AI Financial Model blog.