This post explains how to calculate delta sensitivities or delta vector of interest rate swap. Delta can be calculated by either 1) zero delta or 2) market delta. To the best of our knowledge, FRTB can use these two methods but SIMM use the market Greeks. We implement R code for two approaches.
Introduction
For detailed information about the Libor IRS swap pricing and zero curve bootstrapping, refer to the following posts.
- Interest Rate Swap Pricing using R code
- Bootstrapping the Zero Curve from IRS Swap Rates using R code
In previous posts, we have priced a 5Y Libor IRS swap and generated a zero curve from market swap rates by using bootstrapping. Based on these works, we calculate Greeks of IRS. Since IRS does not have any option characteristics, our focus is to calculate the delta sensitivities or delta vector. And for convenience, swap value is defined as (floating leg – fixed leg).
Delta Sensitivity
ISDA SIMM uses the following definitions of interest rate risk delta (xx is a risk factor). There are, of course, several versions of it but they are all essentially the same.
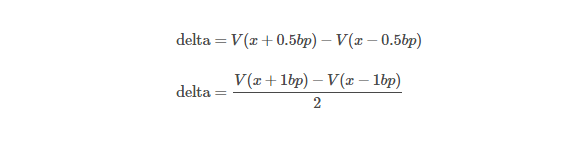
For ease of notation, let z(t) and s(t) denote the (bootstrapped) zero rates or zero curve and (market observed) swap rates or swap curve at time t respectively.
There are two approaches for the calculation of delta: 1) zero delta, 2) market delta.
Zero Delta
Zero delta approach calculates delta sensitivities by bumping up or down zero rates one by one in order.
Once the zero curve (z(t)) is generated from market swap rates (s(t)),
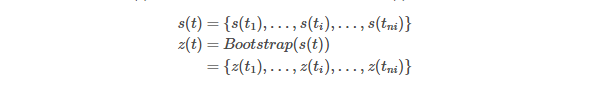
Bumping up (z(t; ti + 0.5bp) or down (z(t; ti−0.5bp)), delta(ti) is calculated and this process is applied for all ti.
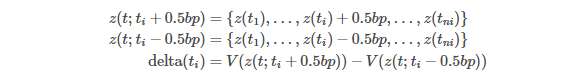
Here, ti, i = 1, 2,…, ni = 1, 2,…, n i are maturities or dates of market swap rates at which the corresponding zero rates are bootstrapped.
Market Delta
Market delta approach calculates delta sensitivities by bumping up or down market swap rates one by one in order. Unlike the zero delta, every time we bump one market swap rate of a selected maturity, we should run a bootstrapping for finding new zero curve. Using this newly generated zero curve, we can calculate delta sensitivity at time ti as follows.
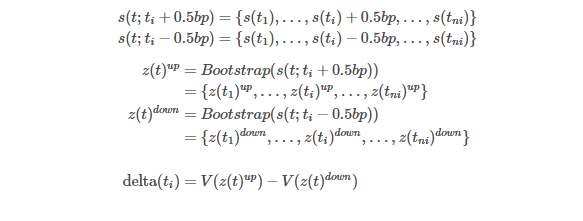
The following R code calculates delta sensitivities of IRS using these two approaches.
#=========================================================================#
# Financial Econometrics & Derivatives, ML/DL using R, Python, Tensorflow
# by Sang-Heon Lee
#
# https://kiandlee.blogspot.com
#————————————————————————-#
# Calculate Delta Sensitivities of Libor IRS
#=========================================================================#
graphics.off() # clear all graphs
rm(list = ls()) # remove all files from your workspace
#=========================================================================
# Functions – Definition
#=========================================================================
#————————————————————–
# Calculation of IRS swap price
#————————————————————–
f_zero_prr_IRS <– function(
fixed_rate, # fixed rate
vd.fixed_date, vd.float_date, # date for two legs
vd.zero_date, v.zero_rate, # zero curve (dates, rates)
d.spot_date, no_amt, # spot date, nominal amt
save_cf_yn) { # “y” : CF save
#———————————————————-
# 0) Preprocessing
#———————————————————-
# convert spot date from date(d) to numeric(n)
n.spot_date <– as.numeric(d.spot_date)
# Interpolation of zero curve
vn.zero_date <– as.numeric(vd.zero_date)
f_linear <– approxfun(vn.zero_date, v.zero_rate,
method=“linear”)
vn.zero_date.inter <– n.spot_date:max(vn.zero_date)
v.zero_rate.inter <– f_linear(vn.zero_date)
# number of CFs
ni <– length(vd.fixed_date)
nj <– length(vd.float_date)
# output data.frame with CF dates and its interpolated zero
df.fixed = data.frame(d.date = vd.fixed_date,
n.date = as.numeric(vd.fixed_date))
df.float = data.frame(d.date = vd.float_date,
n.date = as.numeric(vd.float_date))
#———————————————————-
# 1) Fixed Leg
#———————————————————-
# zero rate for discounting
df.fixed$zero_DC = f_linear(as.numeric(df.fixed$d.date))
# discount factor
df.fixed$DF <– exp(–df.fixed$zero_DC*
(df.fixed$n.date–n.spot_date)/365)
# tau, CF
for(i in 1:ni) {
ymd <– df.fixed$d.date[i]
ymd_prev <– df.fixed$d.date[i–1]
if(i==1) ymd_prev <– d.spot_date
d <– as.numeric(strftime(ymd, format = “%d”))
m <– as.numeric(strftime(ymd, format = “%m”))
y <– as.numeric(strftime(ymd, format = “%Y”))
d_prev <– as.numeric(strftime(ymd_prev, format = “%d”))
m_prev <– as.numeric(strftime(ymd_prev, format = “%m”))
y_prev <– as.numeric(strftime(ymd_prev, format = “%Y”))
# 30I/360
tau <– (360*(y–y_prev) + 30*(m–m_prev) + (d–d_prev))/360
# cash flow rate
df.fixed$rate[i] <– fixed_rate
# Cash flow at time ti
df.fixed$CF[i] <– fixed_rate*tau*no_amt # day fraction
}
# Present value of CF
df.fixed$PV = df.fixed$CF*df.fixed$DF
#———————————————————-
# 2) Floating Leg
#———————————————————-
# zero rate for discounting
df.float$zero_DC = f_linear(as.numeric(df.float$d.date))
# discount factor
df.float$DF <– exp(–df.float$zero_DC*
(df.float$n.date–n.spot_date)/365)
# tau, forward rate, CF
for(i in 1:nj) {
date <– df.float$n.date[i]
date_prev <– df.float$n.date[i–1]
DF <– df.float$DF[i]
DF_prev <– df.float$DF[i–1]
if(i==1) {
date_prev <– n.spot_date
DF_prev <– 1
}
# ACT/360
tau <– (date – date_prev)/360
# forward rate
fwd_rate <– (1/tau)*(DF_prev/DF–1)
# cash flow rate
df.float$rate[i] <– fwd_rate
# Cash flow amount at time ti
df.float$CF[i] <– fwd_rate*tau*no_amt # day fraction
}
# Present value of CF
df.float$PV = df.float$CF*df.float$DF
# check for cash flows
if (save_cf_yn == “y”) {
# print(df.float); print(df.fixed)
write.csv(df.float, “CF_float.csv”)
write.csv(df.fixed, “CF_fixed.csv”)
}
return(sum(df.float$PV) – sum(df.fixed$PV))
}
#————————————————————–
# IRS swap zero curve generator
#————————————————————–
f_zero_maker_IRS <– function(
df.mt, # market information data.frame
# [d.date, swap_rate, source]]
v.unknown_swap_maty_all, # all unknown swap maturity
vd.fixed_date, # date for fixed leg
vd.float_date, # date for float leg
d.spot_date, # spot date
no_amt) { # nominal principal amount
# convert spot date from date(d) to numeric(n)
n.spot_date <– as.numeric(d.spot_date)
# for bootstrapped zero curve
df.zr <– data.frame(
d.date = df.mt$d.date,
n.date = as.numeric(df.mt$d.date),
tau = as.numeric(df.mt$d.date) – n.spot_date,
taui = as.numeric(df.mt$d.date) – n.spot_date,
swap_rate = df.mt$swap_rate,
zero_rate = rep(0,length(df.mt$d.date)),
DF = rep(0,length(df.mt$d.date)))
# tau(i) = t(i) – t(i-1)
df.zr$taui[2:nrow(df.zr)] <–
df.zr$n.date[2:nrow(df.zr)] –
df.# semi-annual date[1: (nrow(df.zr)–1)]
# divide rows according to its source or instrument type
rows_deposit <– which(df.mt$source==“deposit”)
rows_futures <– which(df.mt$source==“futures”)
rows_swap <– which(df.mt$source==“swap”)
#————————————————————–
# 3. Bootstrapping – Deposit
#————————————————————–
for(i in rows_deposit) {
# 1) calculate discount factor for deposit
df.zr$DF[i] <– 1/(1+df.zr$swap_rate[i]*df.zr$tau[i]/360)
# 2) convert DF to spot rate
df.zr$zero_rate[i] <– 365/df.zr$tau[i]*log(1/df.zr$DF[i])
}
#————————————————————–
# 4. Bootstrapping – Futures
#————————————————————–
# No convexity adjustment is made
for(i in rows_futures) {
# 1) discount factor from t(i-1) to t(i)
df.zr$DF[i] <– 1/(1+df.zr$swap_rate[i]*df.zr$taui[i]/360)
# 2) discount factor from spot date to t(i)
df.zr$DF[i] <– df.zr$DF[i–1]*df.zr$DF[i]
# 3) zero rate from discount factor
df.zr$zero_rate[i] <– 365/df.zr$tau[i]*log(1/df.zr$DF[i])
}
#————————————————————–
# 5. Bootstrapping – Swaps
#————————————————————–
k <– 1
for(i in rows_swap) {
# unknown swap maturity in year
swap_maty <– v.unknown_swap_maty_all[k]
# 1) find one unknown zero rate for one swap maturity
m<–optim(0.01, objf,
control = list(abstol=10^(–20), reltol=10^(–20),
maxit=50000, trace=2),
method = c(“Brent”),
lower = 0, upper = 0.1, # for Brent
v.unknown_swap_maty = swap_maty, # unknown zero maturity
v.swap_rate = df.zr$swap_rate[i], # observed swap rate
vd.fixed_date = vd.fixed_date, # date for fixed leg
vd.float_date = vd.float_date, # date for float leg
vd.zero_date_all = df.zr$d.date[1:i], # all dates for zero curve
v.zero_rate_known = df.zr$zero_rate[1: (i–1)], # known zero rates
d.spot_date = d.spot_date,
no_amt = no_amt)
# 2) update this zero curve with the newly found zero rate
df.zr$zero_rate[i] <– m$par
# 3) convert this new zero rate to discount factor
df.zr$DF[i] <– exp(–df.zr$zero_rate[i]*df.zr$tau[i]/365)
k <– k + 1
}
return(df.zr)
}
#————————————————————–
# objective function to be minimized
#————————————————————–
objf <– function(
v.unknown_swap_zero_rate, # unknown zero curve (rates)
v.unknown_swap_maty, # unknown swap maturity
v.swap_rate, # fixed rate
vd.fixed_date, # date for fixed leg
vd.float_date, # date for float leg
vd.zero_date_all, # all dates for zero curve
v.zero_rate_known, # known zero curve (rates)
d.spot_date, # spot date
no_amt) { # nominal principal amount
# zero curve augmented with zero rates for swaps
v.zero_rate_all <– c(v.zero_rate_known,
v.unknown_swap_zero_rate)
v.swap_pr <– NULL # vector of swap prices
k <– 1
for(i in v.unknown_swap_maty) {
# calculate IRS swap price
swap_pr <– f_zero_prr_IRS(
v.swap_rate[k], # fixed rate,
vd.fixed_date[1: (2*i)], # semi-annual date
vd.float_date[1: (4*i)], # quarterly date
vd.zero_date_all, # zero curve (dates)
v.zero_rate_all, # zero curve (rates)
d.spot_date, no_amt, “n”)
# concatenate swap prices
v.swap_pr <– c(v.swap_pr, swap_pr)
k <– k + 1
}
return(sum(v.swap_pr^2))
}
#=========================================================================
# Main
#=========================================================================
#————————————————————–
# 1. Market Information
#————————————————————–
# Zero curve from Bloomberg as of 2021-06-30 until 5-year maturity
df.mt <– data.frame(
d.date = as.Date(c(“2021-10-04”,“2021-12-15”,
“2022-03-16”,“2022-06-15”,
“2022-09-21”,“2022-12-21”,
“2023-03-15”,“2023-07-03”,
“2024-07-02”,“2025-07-02”,
“2026-07-02”)),
# we use swap rate not zero rate.
swap_rate= c(0.00145750000000000,
0.00139609870272047,
0.00203838571440434,
0.00197747863867587,
0.00266249271921742,
0.00359490949297661,
0.00512603194652204,
0.00328354999423027,
0.00571049988269806,
0.00793000012636185,
0.00964949995279312
),
source = c(“deposit”, rep(“futures”,6), rep(“swap”, 4))
)
#————————————————————–
# 2. Libor Swap Specification
#————————————————————–
d.spot_date <– as.Date(“2021-07-02”) # spot date (date type)
n.spot_date <– as.numeric(d.spot_date) # spot date (numeric type)
no_amt <– 10000000 # notional principal amount
# swap cash flow schedule from Bloomberg
lt.cf_date <– list(
fixed = as.Date(c(“2022-01-04”,“2022-07-05”,
“2023-01-03”,“2023-07-03”,
“2024-01-02”,“2024-07-02”,
“2025-01-02”,“2025-07-02”,
“2026-01-02”,“2026-07-02”)),
float = as.Date(c(“2021-10-04”,“2022-01-04”,
“2022-04-04”,“2022-07-05”,
“2022-10-03”,“2023-01-03”,
“2023-04-03”,“2023-07-03”,
“2023-10-02”,“2024-01-02”,
“2024-04-02”,“2024-07-02”,
“2024-10-02”,“2025-01-02”,
“2025-04-02”,“2025-07-02”,
“2025-10-02”,“2026-01-02”,
“2026-04-02”,“2026-07-02”))
)
#————————————————————–
# 3. 5-year swap price : base
#————————————————————–
i = 5 # 5-year swap
# zero pricing
df.zr <– f_zero_maker_IRS(
df.mt, c(2,3,4,5),
lt.cf_date$fixed, lt.cf_date$float,
d.spot_date, no_amt)
pr <– f_zero_prr_IRS(
df.mt$swap_rate[i+6],
lt.cf_date$fixed[1: (2*i)],
lt.cf_date$float[1: (4*i)],
df.zr$d.date, df.zr$zero_rate,
d.spot_date,no_amt, save_cf_yn = “y”)
print(paste0(i,“-year Swap price at spot date = “, pr))
df.zr_delta <– df.mt_delta <– df.zr[,–c(2,3,4)]
df.zr_delta$pr <– df.mt_delta$pr <– pr
#————————————————————–
# 3. Bump and Reprice for Market Greeks
#————————————————————–
df.mt_delta$delta <– df.mt_delta$pr_up <– df.mt_delta$pr_dn <– NA
# iteration for all market maturities
for(r in 1:11) {
#———————
# bump up (1bp up)
#———————
df.mt_bump <– df.mt # initialization
df.mt_bump$swap_rate[r] <– df.mt_bump$swap_rate[r] + 0.0001
# zero pricing
df.zr <– f_zero_maker_IRS(df.mt_bump, c(2,3,4,5),
lt.cf_date$fixed, lt.cf_date$float,
d.spot_date, no_amt)
pr <– f_zero_prr_IRS(df.mt$swap_rate[i+6],
lt.cf_date$fixed[1: (2*i)],
lt.cf_date$float[1: (4*i)],
df.zr$d.date, df.zr$zero_rate,
d.spot_date, no_amt, “n”)
# save price with bumping up
df.mt_delta$pr_up[r] <– pr
# check whether swap prices at spot date is at par
pr <– f_zero_prr_IRS(df.mt_bump$swap_rate[i+6],
lt.cf_date$fixed[1: (2*i)],
lt.cf_date$float[1: (4*i)],
df.zr$d.date, df.zr$zero_rate,
d.spot_date,no_amt, “n”)
print(paste0(i,“-year Swap price at spot date = “, pr))
#———————
# bump down (1bp down)
#———————
df.mt_bump <– df.mt # initialization
df.mt_bump$swap_rate[r] <– df.mt_bump$swap_rate[r] – 0.0001
# zero pricing
df.zr <– f_zero_maker_IRS(df.mt_bump, c(2,3,4,5),
lt.cf_date$fixed, lt.cf_date$float,
d.spot_date, no_amt)
pr <– f_zero_prr_IRS(df.mt$swap_rate[i+6],
lt.cf_date$fixed[1: (2*i)], lt.cf_date$float[1: (4*i)],
df.zr$d.date, df.zr$zero_rate, d.spot_date,no_amt, “n”)
# save price with bumping down
df.mt_delta$pr_dn[r] <– pr
# check whether swap prict at spot date is at par
pr <– f_zero_prr_IRS(df.mt_bump$swap_rate[i+6],
lt.cf_date$fixed[1: (2*i)], lt.cf_date$float[1: (4*i)],
df.zr$d.date, df.zr$zero_rate, d.spot_date,no_amt, “n”)
print(paste0(i,“-year Swap price at spot date = “, pr))
}
# Market Greeks : Delta calculation
df.mt_delta$delta <– (df.mt_delta$pr_up –
df.mt_delta$pr_dn)/2
df.mt_delta
x11(width = 5, height = 3.5)
barplot(delta ~ substr(d.date,1,7), data = df.mt_delta,
width = 0.5, col = “blue”)
x11(width = 5, height = 3.5)
barplot(delta ~ substr(d.date,1,7), data = df.mt_delta[1:10,],
width = 0.5, col = “green”)
#————————————————————–
# 4. Bump and Reprice for Zero Greeks
#————————————————————–
df.zr_delta$delta <– df.zr_delta$pr_up <– df.zr_delta$pr_dn <– NA
# zero pricing
df.zr <– f_zero_maker_IRS(df.mt, c(2,3,4,5),
lt.cf_date$fixed, lt.cf_date$float, d.spot_date, no_amt)
for(r in 1:11) {
#———————
# bump up (1bp up)
#———————
df.zr_bump <– df.zr # initialization
df.zr_bump$zero_rate[r] <– df.zr_bump$zero_rate[r] + 0.0001
# zero pricing
pr <– f_zero_prr_IRS(df.mt$swap_rate[i+6],
lt.cf_date$fixed[1: (2*i)], lt.cf_date$float[1: (4*i)],
df.zr_bump$d.date, df.zr_bump$zero_rate,
d.spot_date, no_amt, “n”)
# save price with bumping up
df.zr_delta$pr_up[r] <– pr
#———————
# bump down (1bp down)
#———————
df.zr_bump <– df.zr # initialization
df.zr_bump$zero_rate[r] <– df.zr_bump$zero_rate[r] – 0.0001
# zero pricing
pr <– f_zero_prr_IRS(df.mt$swap_rate[i+6],
lt.cf_date$fixed[1: (2*i)], lt.cf_date$float[1: (4*i)],
df.zr_bump$d.date, df.zr_bump$zero_rate,
d.spot_date,no_amt, “n”)
# save price with bumping down
df.zr_delta$pr_dn[r] <– pr
}
# Market Greeks : Delta calculation
df.zr_delta$delta <– (df.zr_delta$pr_up –
df.zr_delta$pr_dn)/2
df.zr_delta
x11(width = 5, height = 3.5)
barplot(delta ~ substr(d.date,1,7), data = df.zr_delta,
width = 0.5, col = “blue”)
x11(width = 5, height = 3.5)
barplot(delta ~ substr(d.date,1,7), data = df.zr_delta[1:10,],
width = 0.5, col = “green”)
Colored by Color Scripter
Stay tuned for the next installment to learn about the output demonstrating zero delta vector along the maturities.
For additional insight on this topic and to download the R scripts, visit https://kiandlee.blogspot.com/2021/07/delta-sensitivity-of-interest-rate-swap.html.
Disclosure: Interactive Brokers
Information posted on IBKR Campus that is provided by third-parties does NOT constitute a recommendation that you should contract for the services of that third party. Third-party participants who contribute to IBKR Campus are independent of Interactive Brokers and Interactive Brokers does not make any representations or warranties concerning the services offered, their past or future performance, or the accuracy of the information provided by the third party. Past performance is no guarantee of future results.
This material is from SHLee AI Financial Model and is being posted with its permission. The views expressed in this material are solely those of the author and/or SHLee AI Financial Model and Interactive Brokers is not endorsing or recommending any investment or trading discussed in the material. This material is not and should not be construed as an offer to buy or sell any security. It should not be construed as research or investment advice or a recommendation to buy, sell or hold any security or commodity. This material does not and is not intended to take into account the particular financial conditions, investment objectives or requirements of individual customers. Before acting on this material, you should consider whether it is suitable for your particular circumstances and, as necessary, seek professional advice.









![[Gamma] Scalping Please [Gamma] Scalping Please](https://ibkrcampus.com/wp-content/smush-webp/2024/04/tir-featured-8-700x394.jpg.webp)




