Central Limit Theorem Explained in Python (with Examples) – Part V

See Part I,  Part II , Part III and Part IV to get started.

Example 2 – Binomially distributed population

In the previous example, we knew that the population is exponentially distributed with parameter λλ=0.25.

Now you might wonder what would happen to the sampling distribution if we had a population which followed some other distribution say, Binomial distribution for example.

Would the sampling distribution still resemble the normal distribution for large sample sizes as stated by the CLT?

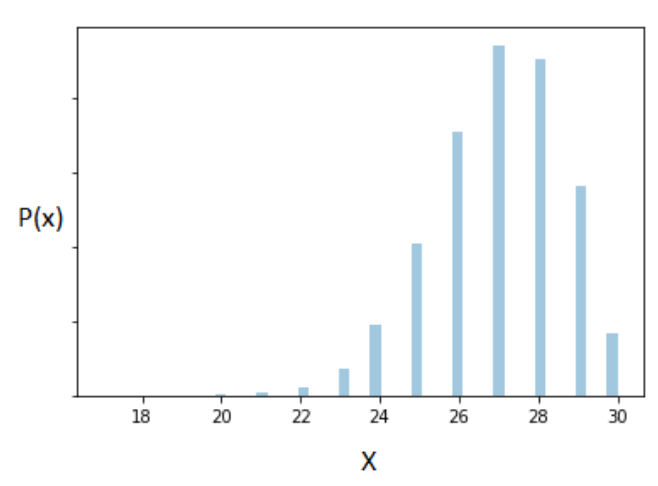
Let’s test it out. The following represents our Binomially distributed population (recall that Binomial is a discrete distribution and hence we produce the probability mass function below):

As before, we follow a similar approach and plot the sampling distribution obtained with a large sample size (n = 500) for a Binomially distributed variable with parameters k=30 and p = 0.9

# drawing 50 random samples of size 500 from a Binomial distribution with parameters k= 30 and p=0.9
sample_size=500

df500 = pd.DataFrame()

for i in range(1, 51):
exponential_sample = np.random.binomial(30,0.9, sample_size)
col = f’sample {i}’
df500[col] = exponential_sample

# Plotting the sampling distribution from a
df500_sample_means_binomial = pd.DataFrame(df500.mean(),columns=[‘Sample means’])
sns.distplot(df500_sample_means_binomial);

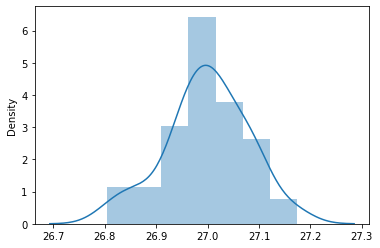
For this example, as we assumed that our population follows a Binomial distribution with parameters k = 30 and p =0.9, which means if CLT were to hold, the sampling distribution should be approximately normal with mean = population mean = μ=27μ=27 and standard deviation = σ/√nσ/n = 0.0734.

# Mean of sample means is close to the population mean
df500_sample_means_binomial.mean().values[0]

26.99175999999999

# Standard deviation of sample means is close to population standard deviation divided by square root of sample size
df500_sample_means_binomial.std().values[0]

0.06752975459086173

And the CLT holds again, as can be seen in the above plot.The sampling distribution for a Binomially distributed population also tends to a normal distribution with mean μ=μ= and standard deviation σ/√nσ/n for large sample size.

Stay tuned for the next installment, in which Ashutosh will go over an application of CLT in investing/trading.

Visit QuantInsti for additional details and to download full code: https://blog.quantinsti.com/central-limit-theorem/.

Disclaimer: All investments and trading in the stock market involve risk. Any decisions to place trades in the financial markets, including trading in stock or options or other financial instruments is a personal decision that should only be made after thorough research, including a personal risk and financial assessment and the engagement of professional assistance to the extent you believe necessary. The trading strategies or related information mentioned in this article is for informational purposes only.