There is a huge number of ways how one can transform financial times-series in order to discover new information about changing price dynamics. We talk here about certain transformation that takes price time-series (or return-series) and transforms it into a new domain. Every solid textbook on Time-Series Analysis lists ample examples.
1. Fourier Transform
Interestingly, there is little to few information on the usefulness of Fourier Transform (FT) applied to financial time-series. No wonder why. In discrete edition of the FT, the incoming time-series, x(t) where t denotes time, is transformed into frequency domain of information, P(f) where f is frequency and P represents effective power of transformed signal, e.g.
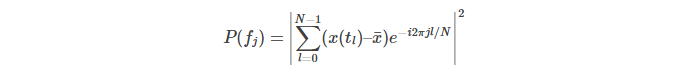
where 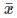 denotes mean values and N number of data points in x(t) and fj is frequency index. The quantity of P(f), defined above, often is referred to as Fourier Power Spectrum. The key information here is what it does. In plain English, the FT scans a wide range of frequencies and matches a degree of similarity between a sine wave of frequency fj and the signal x(tj) itself. If such “correlation” exists, the P (or the inner product between the signal and base sine function) will deliver a large value compared to the other frequencies. In other words, FT is best if we look for purely periodic oscillations in our time-series. The best scenario would be if such periodic pattern is active along the entire record of the examined signal; it loses it power if it lasts shorter under additional condition, i.e. if signal-to-noise ratio allows for its detection. Signal that is a realisation of white noise has a flat power spectrum while time-series with long up/down-trends will reveal lots of colour noise in low frequency section. In a log-log representation of P(f), such colour noise is modelled by a power-law model,
denotes mean values and N number of data points in x(t) and fj is frequency index. The quantity of P(f), defined above, often is referred to as Fourier Power Spectrum. The key information here is what it does. In plain English, the FT scans a wide range of frequencies and matches a degree of similarity between a sine wave of frequency fj and the signal x(tj) itself. If such “correlation” exists, the P (or the inner product between the signal and base sine function) will deliver a large value compared to the other frequencies. In other words, FT is best if we look for purely periodic oscillations in our time-series. The best scenario would be if such periodic pattern is active along the entire record of the examined signal; it loses it power if it lasts shorter under additional condition, i.e. if signal-to-noise ratio allows for its detection. Signal that is a realisation of white noise has a flat power spectrum while time-series with long up/down-trends will reveal lots of colour noise in low frequency section. In a log-log representation of P(f), such colour noise is modelled by a power-law model, 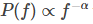 where the higher
where the higher 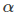 the steeper slope or stronger trend in time-domain of the signal.
the steeper slope or stronger trend in time-domain of the signal.
In real life applications of FT, very rarely trading signals are dominated by distinct periodicities. Due to unlimited market factors, the power spectrum may display broader “peaks”, suggesting the existence of a latent dumping process or 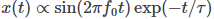 where
where 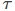 denotes a damping time-scale. In science, we talk about not periodic but a bunch of periodic or localised periodic or quasi-periodic oscillations (QPOs) present in the signal. A Lorentzian has
denotes a damping time-scale. In science, we talk about not periodic but a bunch of periodic or localised periodic or quasi-periodic oscillations (QPOs) present in the signal. A Lorentzian has
defined by a centroid frequency, f0, a full width at half maximum (FWHM) of Δf and amplitude. A ratio of the QPO frequency to Lorentzian FWHM is known as a quality factor, Q = f0/Δf. The distinguishing feature of the QPO as opposed to the noise components is that its quality factor can be large. The higher Q the wider QPO. All these parameters are correlated in the low-frequency QPO, with the amplitude and quality factor increasing along with the increase in centroid frequency.
It is obviously important to know what sets the (lack of) coherence of the QPO. Are QPOs composed of a set of longer-lasting continuous modulations or are they rather fragmented in time with frequencies concentrated around the peak QPO frequency? Is there any correlation between observed oscillations or they are preferably excited in a random manner? To answer these questions we need to resolve and understand the internal structure of detected QPOs i.e. to study the behaviour of the QPO on timescales which are short compared to its observed broadening. A continuous modulation would then show up as a continuous drift in QPO frequency with time, while a series of short timescale oscillations will show up as disjoint sections where the QPO is on and off.
One way to do this is using dynamical power spectra (spectrograms; hereafter also referred to as Short-Fourier Transform or STFT for simplicity). While the actual techniques for this can be quite sophisticated in essence, an observation of length T sampled every Δt (giving a single power spectrum spanning frequencies 1/T to 1/(2Δt) in steps of 1/T) is spilt into N segments of length T/N. This gives N independent power spectra spanning frequencies N/T to 1/(2Δt) but crucially, the resolution is now lower, at N/T. While this is useful in tracing the evolution of the QPO, it introduces “instrumental” frequency broadening from the windowing of the data which prevents us following the detailed behaviour of the QPO on the required timescales.
The real problem with such Fourier analysis techniques is that they decompose the signal onto a basis set of sinusoid functions. These have frequency f, with resolution Δf=N/T, but exist everywhere in time across the duration of the observation Tdur=T/N. In the same way that the Heisenberg uncertainty principle sets a limit to the measurement of momentum and location of a particle, namely ΔpxΔx≥ℎ/2ℼ where ℎ is a Planck constant, there is a Heisenberg-Gabor uncertainty principle setting the limiting frequency resolution for time-series analysis. This states that we cannot determine both the frequency and time location of a power spectral feature with infinite accuracy.
2. Wavelet Transform
Instead, if the QPO is really a short-lived signal, we will gain in resolution and get closer to the theoretical limit by using a set of basis functions which match the underlying physical shape of the QPO. This is the idea behind wavelet analysis. For example, one particular basis function shape is the Morlet wavelet, which is a sinusoid of frequency f, modulated in amplitude by a gaussian envelope such that it lasts only for a duration Tdur. The product f × Tdur is set at a constant, fixing the number of cycles seen in the basis function. The lightcurve is then decomposed on these basis functions, calculated over a set of frequencies so that the basis function shape is maintained (i.e. that the oscillation consists of 4 cycles, so low frequencies have longer Tdur than high frequencies). The resolution adjusts with the frequency, making this a more sensitive technique to follow short duration signals.
However, the problem is that the basis functions chosen in wavelet analysis may not be appropriate. For example, we assumed above that these functions have a fixed shape, lasting for a fixed number of oscillations at all frequencies. In practice, this may not be the best description of the QPO. Perhaps the QPO is made from a set of signals which have a distribution of durations, where f × Tdur is not constant. We will maximise the resolution with which we can look at the QPO if and only if we use basis functions which best match its shape.
To do this one can propose the application of the Matching Pursuit algorithm (MP). This is an iterative method for signal decomposition which aims at retrieving the maximum possible theoretical resolution by deriving the basis functions from the signal itself. We specifically use this as an extension of the wavelet technique by setting the MP basis functions as Gaussian amplitude modulated sinusoids as before, but allowing the product f × Tdur to be a free parameter (a.k.a. Gabor atoms).
3. Matching Pursuit algorithm
Signal time-frequency analysis can be compared to speaking in a foreign language. In each language we use words. Words are needed to express our thoughts, problems, ideas, etc. By a smart selection of proper words we can say and explain whatever we wish. A whole collection of words can be gathered in the form of a dictionary. One can express simple thoughts using a very limited set of words from a huge dictionary (a subset). The same can be applied to a time-series analysis. In order to describe the signal one needs to use a minimum available set of functions − orthonormal basis functions.
Originally posted on Quant at Risk.
Disclosure: Interactive Brokers
Information posted on IBKR Campus that is provided by third-parties does NOT constitute a recommendation that you should contract for the services of that third party. Third-party participants who contribute to IBKR Campus are independent of Interactive Brokers and Interactive Brokers does not make any representations or warranties concerning the services offered, their past or future performance, or the accuracy of the information provided by the third party. Past performance is no guarantee of future results.
This material is from Quant at Risk and is being posted with its permission. The views expressed in this material are solely those of the author and/or Quant at Risk and Interactive Brokers is not endorsing or recommending any investment or trading discussed in the material. This material is not and should not be construed as an offer to buy or sell any security. It should not be construed as research or investment advice or a recommendation to buy, sell or hold any security or commodity. This material does not and is not intended to take into account the particular financial conditions, investment objectives or requirements of individual customers. Before acting on this material, you should consider whether it is suitable for your particular circumstances and, as necessary, seek professional advice.













Join The Conversation
If you have a general question, it may already be covered in our FAQs. If you have an account-specific question or concern, please reach out to Client Services.